Парашютист сразу после прыжка пролетает расстояние 50 м с пренебрежимо

Условие задачи:

Парашютист сразу после прыжка пролетает расстояние 50 м с пренебрежимо малой силой сопротивления воздуха. Далее, после раскрытия парашюта, он движется с ускорением 2 м/с² и достигает земли со скоростью 3 м/с. С какой высоты прыгал парашютист?

Задача №1.4.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h_1=50\) м, \(a=2\) м/с², \(\upsilon=3\) м/с, \(H-?\)

Решение задачи:

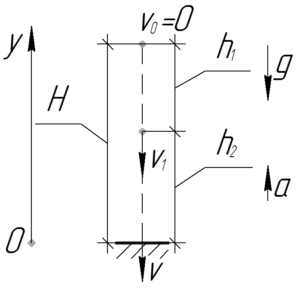Так как парашютист выпрыгнул из самолета без начальной скорости и пролетел расстояние \(h_1\), то найдем сколько времени он на это затратил. Для этого используем формулу:

\[{h_1} = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2{h_1}}}{g}} \]

Теперь найдем скорость \(\upsilon_1\), которую имел парашютист в конце участка свободного падения.

\[{\upsilon _1} = gt\]

Подставим в это выражение полученную выше формулу для времени:

\[{\upsilon _1} = g\sqrt {\frac{{2{h_1}}}{g}}  = \sqrt {2g{h_1}} \]

Далее человек раскрывает парашют и начинает двигаться с ускорением \(a\). Но как: замедленно или ускоренно, т.е. куда направлен вектор ускорения? Чтобы ответить на этот вопрос, сосчитаем скорость \(\upsilon_1\) и сравним ее со скоростью \(\upsilon\) при приземлении.

\[{\upsilon _1} = \sqrt {2 \cdot 10 \cdot 50}  = 31,62\; м/с \]

Так как получилось, что \({\upsilon _1} > \upsilon\), значит парашютист замедлялся. Оно и понятно, так как в противном случае он бы получил травмы при столкновении с землей на большой скорости.

Для участка замедления запишем следующую формулу:

\[{\upsilon ^2} – \upsilon _1^2 =  – 2a{h_2}\]

Отсюда выразим расстояние, которое замедляясь пролетел спортсмен.

\[{h_2} = \frac{{\upsilon _1^2 – {\upsilon ^2}}}{{2a}}\]

Подставим в формулу выражение для \(\upsilon_1\).

\[{h_2} = \frac{{2g{h_1} – {\upsilon ^2}}}{{2a}}\]

Искомую общую высоту \(H\) можно найти как сумму высот \(h_1\) и \(h_2\).

\[H = {h_1} + {h_2}\]

\[H = {h_1} + \frac{{2g{h_1} – {\upsilon ^2}}}{{2a}}\]

Подставим численные данные и вычислим ответ:

\[H = 50 + \frac{{2 \cdot 10 \cdot 50 – {3^2}}}{{2 \cdot 2}} = 297,75 \; м \approx 0,3\; км \]

Ответ: 0,3 км.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.40 Над шахтой глубиной 40 м вертикально вверх бросили камень со скоростью 12 м/с
1.4.42 При падении камня в колодец его удар о поверхность воды доносится через 5 с
1.4.43 Свободно падающий камень пролетел последние три четверти пути за одну