Условие задачи:
Первую половину пути автомобиль двигается со скоростью 60 км/ч, а вторую — со скоростью 40 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
Задача №1.2.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=S_2=\frac{1}{2}S\), \(\upsilon_1=60\) км/ч, \(\upsilon_2=40\) км/ч, \(\upsilon_{ср}-?\)
Решение задачи:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Так как и на первом, и на втором участке автомобиль двигался равномерно, то справедливо записать такую систему.
\[\left\{ \begin{gathered}
{S_1} = {\upsilon _1}{t_1} \hfill \\
{S_2} = {\upsilon _2}{t_2} \hfill \\
\end{gathered} \right.\]
Выразим из каждого выражения время.
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим эти выражения в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{\frac{{{S_1}}}{{{\upsilon _1}}} + \frac{{{S_2}}}{{{\upsilon _2}}}}}\]
По условию \(S_1=S_2=\frac{1}{2}S\), поэтому:
\[{\upsilon _{ср}} = \frac{{\frac{1}{2}S + \frac{1}{2}S}}{{\frac{S}{{2{\upsilon _1}}} + \frac{S}{{2{\upsilon _2}}}}}\]
\[{\upsilon _{ср}} = \frac{S}{{\frac{{S{\upsilon _2} + S{\upsilon _1}}}{{2{\upsilon _1}{\upsilon _2}}}}}\]
\[{\upsilon _{ср}} = \frac{{S \cdot 2{\upsilon _1}{\upsilon _2}}}{{S\left( {{\upsilon _2} + {\upsilon _1}} \right)}}\]
\[{\upsilon _{ср}} = \frac{{2{\upsilon _1}{\upsilon _2}}}{{{\upsilon _1} + {\upsilon _2}}}\]
Подставив в эту итоговую формулу исходные данные задачи, мы получим ответ. Переводить значения скоростей в систему СИ не имеет смысла, подставив их без изменений в формулу, мы получим ответ так же в км/ч.
\[{\upsilon _{ср}} = \frac{{2 \cdot 60 \cdot 40}}{{60 + 40}} = 48\; км/ч = 13,3\; м/с\]
Ответ: 13,3 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.1.11 Точка движется по прямой в одну сторону. На рисунке показан график зависимости
1.2.2 Один автомобиль, двигаясь равномерно со скоростью 12 м/с, в течение 10 с прошел
1.2.3 За минуту человек делает сто шагов. Определить скорость движения человека, если

 icodepro.ru
icodepro.ru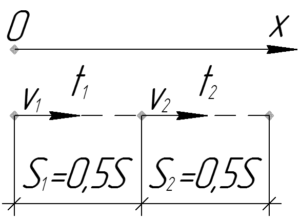
Я также подумал, но к решению не подходил. Спасибо!
Помогите решить пожалуйста
Автомобиль каждые 2 часа проезжал 60 км, постройте график зависимости пройденного пути от времени
Здравствуйте, а такую задачку можно решить?
Первую часть пути автомобиль проехал за 4 сек. со скоростью v1 = 60 км/ч, а вторую за 10 сек. со скоростью v2 = 40 км/ч. Определить среднюю скорость V автомобиля на всем пути.
Здравствуйте, можете решить?
Половину шоссе он проехал со скоростью 60 км/ч, половину оставшегося времени и последнюю половину со скоростью 15 км/ч, а часть со скоростью 45 км/ч. Какова средняя скорость автомобиля на всем пути?
Ваша задача абсолютно аналогична этой, там даже есть видео решение. В Вашем случае ответ должен быть такой:\[{\upsilon _{ср}} = \frac{{2{\upsilon _1}\left( {{\upsilon _2} + {\upsilon _3}} \right)}}{{2{\upsilon _1} + {\upsilon _2} + {\upsilon _3}}}\]\[{\upsilon _{ср}} = \frac{{2 \cdot 60 \cdot \left( {15 + 45} \right)}}{{2 \cdot 60 + 15 + 45}} = 40\;км/ч\]
Корректное условие этой задачи такое: Автомобиль проехал половину пути со скоростью 60 км/ч, оставшуюся часть пути он половину времени ехал со скоростью 15 км/ч , а последний участок со скоростью 45 км/ч. Найдите среднюю скорость автомобиле на всём пути.
Помогите пожалуйста
Два мотоциклиста выехали из пункта А в пункт Б, один половину пути ехал со скоростью 16 км/ч и оставшийся путь шел пешком со скоростью 8 км/ч, а другой – половину времени ехал со скоростью 16 км/ч и половину времени шел пешком со скоростью 8 км/ч. Кто из них доберется в пункт Б быстрее и на сколько, если общее расстояние между пунктами 20 км?
Понятно, что быстрее доберется тот, у кого больше средняя скорость. В первом случае среднюю скорость определяют по формуле:\[{\upsilon _{ср1}} = \frac{{2{\upsilon _1}{\upsilon _2}}}{{{\upsilon _1} + {\upsilon _2}}}\]Во втором случае средняя скорость равна:\[{\upsilon _{ср2}} = \frac{{{\upsilon _1} + {\upsilon _2}}}{2}\]Легко доказать, что во втором случае средняя скорость больше:\[\frac{{{\upsilon _1} + {\upsilon _2}}}{2} \geq \frac{{2{\upsilon _1}{\upsilon _2}}}{{{\upsilon _1} + {\upsilon _2}}}\]\[{\left( {{\upsilon _1} + {\upsilon _2}} \right)^2} \geq 4{\upsilon _1}{\upsilon _2}\]\[\upsilon _1^2 + 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2 \geq 4{\upsilon _1}{\upsilon _2}\]\[\upsilon _1^2 — 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2 \geq 0\]\[{\left( {{\upsilon _1} — {\upsilon _2}} \right)^2} \geq 0\]Теперь посчитаем численное значение времен:\[{t_1} = \frac{S}{{{\upsilon _{ср1}}}} = \frac{{S\left( {{\upsilon _1} + {\upsilon _2}} \right)}}{{2{\upsilon _1}{\upsilon _2}}}\]\[{t_1} = \frac{{20 \cdot \left( {16 + 8} \right)}}{{2 \cdot 16 \cdot 8}} = \frac{{15}}{8}\;ч\]\[{t_2} = \frac{S}{{{\upsilon _{ср2}}}} = \frac{{2S}}{{{\upsilon _1} + {\upsilon _2}}}\]\[{t_2} = \frac{{2 \cdot 20}}{{16 + 8}} = \frac{5}{3}\;ч\]\[\Delta t = {t_1} — {t_2} = \frac{{15}}{8} — \frac{5}{3} = \frac{{45 — 40}}{{24}} = \frac{5}{{24}}\;ч\]
Здравствуйте.
Не могли бы Вы помочь с следующей задачей: Могло ли так случиться, что половину времени поездки спидометр автомобиля показывал 20 вёрст/час, а половину всего пути — 18 вёрст/час? Некоторое время автомобиль мог передвигаться с другими скоростями или стоять на месте.
Ммм, интересная задача. Я решил ее следующим образом.
В моих рассуждения далее \(S\) — полный путь, \(t\) — полное время.
Очень легко доказывается, что автомобиль НЕ мог двигаться только со скоростями \(\upsilon_1=20\) верст/ч и \(\upsilon_2=18\) верст/ч, т.е. обязательно должны присутствовать иные интервалы (времени и расстояния), когда скорость была другой. Почему? Дело в том, что в противном случае скорости на этих двух интервалах должны быть равны друг другу (оба интервала равны по длине \(\frac{S}{2}\) и проходятся за время \(\frac{t}{2}\)), а это противоречит условию задачи.
Далее, с учетом вышесказанного, запишем неравенства для пройденных расстояний и затраченного времени.
Автомобиль едет половину времени поездки со скоростью \(\upsilon_1\), далее проходит половину пути, и сумма пройденных расстояний меньше чем полный путь из-за наличия тех участков, где скорость автомобиля другая, отличная от заданных в условии, поэтому:\[{\upsilon _1}\frac{t}{2} + \frac{S}{2} < S\]\[{\upsilon _1}\frac{t}{2} < \frac{S}{2}\]Получим такое неравенство:\[{\upsilon _1} < \frac{S}{t}\]Также автомобиль затрачивает половину времени, а потом едет половину всего пути со скоростью \(\upsilon_2\), сумма времен должна быть меньше чем полное время по той же причине, что и выше, поэтому:\[\frac{t}{2} + \frac{S}{{2{\upsilon _2}}} < t\]\[\frac{S}{{2{\upsilon _2}}} < \frac{t}{2}\]\[\frac{S}{{{\upsilon _2}}} < t\]\[{\upsilon _2} > \frac{S}{t}\]Теперь внимательно смотрим на полученные неравенства. Понятно, что одно и то же число \(\frac{S}{t}\) не может быть 20 верст/ч и меньше 18 верст/ч, поэтому ответ задачи — нет, такого быть не могло. Интересно, что если \({\upsilon _1} < {\upsilon _2}\), то такое уже возможно.
Большое спасибо! Я шёл примерно в том же направлении, но не дошел

Подскажите отличается ли решение данной задачи, если автомобиль движется по окружности? Спасибо.
Скорее всего нет. Но можете скинуть полное условие Вашей задачи, я обязательно проверю
Помогите пожалуйста с задачей авто двигалось 2 часа первый час 90 км в час а второй 60. Найдите среднюю скорость авто на первой половине пути и на второй
Задача устная. Всего за два часа авто пройдет 150 км (за первый час 90 км, а за второй — 60 км), значит половина пути равна 75 км. Так как первый час авто движется равномерно со скоростью 90 км/ч и проходит 90 км, значит средняя скорость на первой половине пути (поскольку 75 км < 90 км) равна 90 км/ч. Первую половину пути авто пройдет за время, равное 75/90 = 5/6 ч (50 минут). Значит вторую половину авто пройдет уже за время 2-(5/6)=7/6 ч. Средняя скорость на второй половине равна: 75/(7/6)=64,3 км/ч.
Извините, а вы не подскажите как решить? В течение первой секунды от начала движения ускорение грузовика было 6,0 м/с2, в каждую последующую секунду ускорение убывало на 60%. Какова средняя скорость автомобиля за первые 8 с движения?
Среднюю скорость будем определять по формуле:\[{\upsilon _{ср}} = \frac{S}{t}\]Буду решать из предположения, что в течение каждой секунды ускорение остается постоянным и меняется скачкообразно при переходе к следующей секунде (сомневаюсь, что при другом условии эту задачу вообще можно решить аналитически). Далее приму следующие обозначения: \(S_n\) — путь за \(n\)-ую секунду, \(\upsilon_n\) — скорость в начале \(n\)-ой секунды, \(a_n\) — ускорение в течение \(n\)-ой секунды, \(\tau\) — время, равное одной секунде. Сразу отметим, что \(\upsilon_1=0\), а \(a_1=6\) м/с2. Введем коэффициент \(\alpha=0,4\), показывающий во сколько раз изменяется ускорение каждую секунду (если ускорение падает на 60%, значит в следующую секунду ускорение составит 0,4 ускорения в текущую секунду). Запишем формулы для определения пути, пройденное грузовиком в течение каждой из четырех первых секунд движения:\[\left\{ \begin{gathered}

{S_1} = {\upsilon _1}\tau + \frac{{{a_1}{\tau ^2}}}{2} \hfill \\
{S_2} = {\upsilon _2}\tau + \frac{{{a_2}{\tau ^2}}}{2} \hfill \\
{S_3} = {\upsilon _3}\tau + \frac{{{a_3}{\tau ^2}}}{2} \hfill \\
{S_4} = {\upsilon _4}\tau + \frac{{{a_4}{\tau ^2}}}{2} \hfill \\
\end{gathered} \right.\]Разберемся сначала с ускорением:\[\left\{ \begin{gathered}
{a_2} = \alpha {a_1} \hfill \\
{a_3} = \alpha {a_2} = {\alpha ^2}{a_1} \hfill \\
{a_4} = \alpha {a_3} = {\alpha ^3}{a_1} \hfill \\
\end{gathered} \right.\]Легко заметить, что:\[{a_n} = {\alpha ^{n — 1}}{a_1}\]Теперь перейдем к скоростям:\[\left\{ \begin{gathered}
{\upsilon _2} = {\upsilon _1} + {a_1}\tau = {a_1}\tau \hfill \\
{\upsilon _3} = {\upsilon _2} + {a_2}\tau = {a_1}\tau + {a_2}\tau \hfill \\
{\upsilon _4} = {\upsilon _3} + {a_3}\tau = {a_1}\tau + {a_2}\tau + {a_3}\tau \hfill \\
\end{gathered} \right.\]Учитывая выражения для ускорения, имеем:\[\left\{ \begin{gathered}
{\upsilon _2} = {a_1}\tau \hfill \\
{\upsilon _3} = {a_1}\tau + \alpha {a_1}\tau = {a_1}\tau \left( {1 + \alpha } \right) \hfill \\
{\upsilon _4} = {a_1}\tau + \alpha {a_1}\tau + {\alpha ^2}{a_1}\tau = {a_1}\tau \left( {1 + \alpha + {\alpha ^2}} \right) \hfill \\
\end{gathered} \right.\]Так как в скобках сумма первых членов геометрической прогрессии, то можно получить следующую формулу:\[{\upsilon _n} = {a_1}\tau \frac{{\left( {1 — {\alpha ^{n — 1}}} \right)}}{{1 — \alpha }}\]Тогда путь за \(n\)-ую секунду следует искать по формуле:\[{S_n} = {\upsilon _n}\tau + \frac{{{a_n}{\tau ^2}}}{2} = {a_1}{\tau ^2}\frac{{\left( {1 — {\alpha ^{n — 1}}} \right)}}{{1 — \alpha }} + \frac{{{\alpha ^{n — 1}}{a_1}{\tau ^2}}}{2}\]Упростим:\[{S_n} = \frac{{{a_1}{\tau ^2}}}{2}\left( {\frac{{2\left( {1 — {\alpha ^{n — 1}}} \right)}}{{1 — \alpha }} + \frac{{\left( {1 — \alpha } \right){\alpha ^{n — 1}}}}{{1 — \alpha }}} \right)\]\[{S_n} = \frac{{{a_1}{\tau ^2}}}{2} \cdot \frac{{2 — 2{\alpha ^{n — 1}} + {\alpha ^{n — 1}} — {\alpha ^n}}}{{1 — \alpha }}\]\[{S_n} = \frac{{{a_1}{\tau ^2}}}{2} \cdot \frac{{2 — {\alpha ^{n — 1}} — {\alpha ^n}}}{{1 — \alpha }}\]\[{S_n} = \frac{{{a_1}{\tau ^2}}}{2}.\frac{{{\alpha ^n} + {\alpha ^{n — 1}} — 2}}{{\alpha — 1}}\]Тогда для первых восьми секунд имеем:\[\left\{ \begin{gathered}
{S_1} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 1 \hfill \\
{S_2} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 2,4 \hfill \\
{S_3} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 2,96 \hfill \\
{S_4} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 3,184 \hfill \\
{S_5} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 3,2736 \hfill \\
{S_6} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 3,30944 \hfill \\
{S_7} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 3,323776 \hfill \\
{S_8} = \frac{{{a_1}{\tau ^2}}}{2} \cdot 3,3295104 \hfill \\
\end{gathered} \right.\]Путь за первые восемь секунд равен:\[S = \sum\limits_{n = 1}^8 {{S_n}} = 22,7803264 \cdot \frac{{{a_1}{\tau ^2}}}{2}\]Средняя скорость равна:\[{\upsilon _{ср}} = 22,7803264 \cdot \frac{{{a_1}{\tau ^2}}}{{2t}}\]Численный ответ равен:\[{\upsilon _{11}} = 22,7803264 \cdot \frac{{6 \cdot {1^2}}}{{2 \cdot 8}} = 8,5\;м/с = 30,6\;км/ч\]К сожалению, мой ответ не совпал с ответом, который я нашёл в интернете
Если найдете ошибку, пожалуйста, сообщите
Извините за беспокойство, но не подскажите как решить? Мотоциклист полпути ехал со скоростью 90км/ч, а вторую половину пути 60 км/ч, какова средняя скорость мотоциклиста. Заранее спасибо!
Абсолютно такая же задача, просто другие численные данные. Ответ будет такой:\[{\upsilon _{кв}} = \frac{{2 \cdot 90 \cdot 60}}{{90 + 60}} = 72\;км/ч\]
А почему вы умножает на 2 в этой задаче? Ответе пожалуйста.
Так получилось в ходе решения задачи. Я даже видео записал, можете посмотреть
Как решить задачу если дано 3 скорость (как и этот задача)18км/час 36 и 72
Вероятно решение такой задачи будет аналогично решению этой
подскажите пожалуйста.
как найти V2 если известно V1 и средняя скорсть?
Решаете также, пока не получите формулу:\[{\upsilon _{ср}} = \frac{{2{\upsilon _1}{\upsilon _2}}}{{{\upsilon _1} + {\upsilon _2}}}\]Далее отсюда нужно выразить \(\upsilon_2\), что я и проделаю:\[{\upsilon _{ср}}\left( {{\upsilon _1} + {\upsilon _2}} \right) = 2{\upsilon _1}{\upsilon _2}\]\[{\upsilon _{ср}}{\upsilon _1} + {\upsilon _{ср}}{\upsilon _2} = 2{\upsilon _1}{\upsilon _2}\]\[{\upsilon _{ср}}{\upsilon _1} = {\upsilon _2}\left( {2{\upsilon _1} — {\upsilon _{ср}}} \right)\]Окончательно имеем:\[{\upsilon _2} = \frac{{{\upsilon _{ср}}{\upsilon _1}}}{{2{\upsilon _1} — {\upsilon _{ср}}}}\]
А можете объяснить, как мы получим окончательный ответ этой формулы?
Известно, что произведение двух множителей A и B дают некоторое произведение C. Чтобы найти множитель A, нужно произведение C разделить на множитель B.
Надеюсь правильно понял Ваш вопрос
Помогите Пожалуйста


Турист половину пути проехал на автомобиле со скоростью v1 = 76 км/час. Затем половину оставшегося времени он ехал на велосипеде со скоростью v2 = 18 км/час, а потом до конца пути шел пешком со скоростью v3 = 6 км/час. Определите среднюю скорость туриста на всем пути.
Посмотрите решение аналогичной задачи, там просто цифры другие
Помогите пожалуйста!!!Первую четверть пути автомобиль проезжает по лесной дороге со скоростью 40 км/ч, а оставшуюся часть пути – по сельской дороге со скоростью 60 км/ч. Вычислите среднюю скорость автомобиля на всём пути.
Укажите ответ в км/ч.
\[t = {t_1} + {t_2} = \frac{S}{{4{\upsilon _1}}} + \frac{{3S}}{{4{\upsilon _2}}} = \frac{{S{\upsilon _2} + 3S{\upsilon _1}}}{{4{\upsilon _1}{\upsilon _2}}} = \frac{{S\left( {3{\upsilon _1} + {\upsilon _2}} \right)}}{{4{\upsilon _1}{\upsilon _2}}}\]\[{\upsilon _{ср}} = \frac{S}{t} = \frac{{S \cdot 4{\upsilon _1}{\upsilon _2}}}{{S\left( {3{\upsilon _1} + {\upsilon _2}} \right)}} = \frac{{4{\upsilon _1}{\upsilon _2}}}{{3{\upsilon _1} + {\upsilon _2}}}\]\[{\upsilon _{ср}} = \frac{{4 \cdot 40 \cdot 60}}{{3 \cdot 40 + 60}} = 53,33\;км/ч\]
Помогите, пожалуйста. Буду очень благодарна, заранее спасибо. 1) Первую половину пути автомобиль прошёл со скоростью 60 км/ч, а оставшийся путь-со скоростью 25 м/с. Определите среднюю скорость автомобиля на всём пути. P.s. Ответ должен быть — 72 км/ч. Думаю, задача простая, но у меня никак не получается)
2) Половину времени движения автомобиль ехал со скоростью 60 км/ч, а оставшееся время — со скоростью 25м/с. Чему равна средняя линия скорость автомобиля на всём пути? Опять же, ответ должен быть-75 км/ч.
3) Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ должен быть — 36 км/ч.
4) Пешеход часть пути прошёл со скоростью 5 км/ч, затратив на это две трети времени своего движения. За оставшееся время он прошёл остальной путь со скоростью, равной 8 /км/ч. Определите среднюю скорость пешехода на всём пути. Ответ должен быть — 6 км/ч.
Привожу решения без подробных объяснений.
Первая задача:\[t = \frac{S}{{2{\upsilon _1}}} + \frac{S}{{2{\upsilon _2}}} = \frac{{S\left( {{\upsilon _1} + {\upsilon _2}} \right)}}{{2{\upsilon _1}{\upsilon _2}}}\]\[{\upsilon _{ср}} = \frac{S}{t} = \frac{{S \cdot 2{\upsilon _1}{\upsilon _2}}}{{S\left( {{\upsilon _1} + {\upsilon _2}} \right)}} = \frac{{2{\upsilon _1}{\upsilon _2}}}{{{\upsilon _1} + {\upsilon _2}}}\]\[{\upsilon _{ср}} = \frac{{2 \cdot 60 \cdot 90}}{{60 + 90}} = 72\;км/ч\]Напомню, что 25 м/с = 90 км/ч.
Вторая задача:\[S = {\upsilon _1} \cdot \frac{t}{2} + {\upsilon _2} \cdot \frac{t}{2} = \frac{{\left( {{\upsilon _1} + {\upsilon _2}} \right)t}}{2}\]\[{\upsilon _{ср}} = \frac{S}{t} = \frac{{\left( {{\upsilon _1} + {\upsilon _2}} \right)t}}{{2t}} = \frac{{{\upsilon _1} + {\upsilon _2}}}{2}\]\[{\upsilon _{ср}} = \frac{{60 + 90}}{2} = 75\;км/ч\]Также используется, что 25 м/с = 90 км/ч.
Третья задача:\[t = \frac{S}{{4{\upsilon _1}}} + \frac{{3S}}{{4{\upsilon _2}}} = \frac{{S\left( {{\upsilon _2} + 3{\upsilon _1}} \right)}}{{4{\upsilon _1}{\upsilon _2}}}\]\[{\upsilon _{ср}} = \frac{S}{t} = \frac{{S \cdot 4{\upsilon _1}{\upsilon _2}}}{{S\left( {{\upsilon _2} + 3{\upsilon _1}} \right)}} = \frac{{4{\upsilon _1}{\upsilon _2}}}{{{\upsilon _2} + 3{\upsilon _1}}}\]Тогда:\[{\upsilon _{ср}}\left( {{\upsilon _2} + 3{\upsilon _1}} \right) = 4{\upsilon _1}{\upsilon _2}\]Раскроем скобки:\[{\upsilon _{ср}}{\upsilon _2} + 3{\upsilon _{ср}}{\upsilon _1} = 4{\upsilon _1}{\upsilon _2}\]Группируем:\[3{\upsilon _{ср}}{\upsilon _1} = {\upsilon _2}\left( {4{\upsilon _1} — {\upsilon _{ср}}} \right)\]Откуда имеем:\[{\upsilon _2} = \frac{{3{\upsilon _{ср}}{\upsilon _1}}}{{4{\upsilon _1} — {\upsilon _{ср}}}}\]\[{\upsilon _2} = \frac{{3 \cdot 40 \cdot 60}}{{4 \cdot 60 — 40}} = 36\;км/ч\]
Четвертая задача:\[S = {\upsilon _1} \cdot \frac{{2t}}{3} + {\upsilon _2} \cdot \frac{t}{3} = \frac{{\left( {2{\upsilon _1} + {\upsilon _2}} \right)t}}{3}\]\[{\upsilon _{ср}} = \frac{S}{t} = \frac{{\left( {2{\upsilon _1} + {\upsilon _2}} \right)t}}{{3t}} = \frac{{2{\upsilon _1} + {\upsilon _2}}}{3}\]\[{\upsilon _{ср}} = \frac{{2 \cdot 5 + 8}}{3} = 6\;км/ч\]
Спасибо огромное, даже не знаю, как вас благодарить)?
Одну четвертую часть времени автомобиль ехал со скоростью 20 км/ч, а оставшуюся часть дороги — со скоростью 60 км/ч. Наити среднюю скорость (км/ч) автомобиля на всем пути. Округлите до целых
Одну четвертую часть пути автомобиль ехал со скоростью 20 км/ч, а оставшуюся часть дороги — со скоростью 60 км/ч. Наити среднюю скорость (км/ч) автомобиля на всем пути. Округлите до целых
Для решения обеих задач будем использовать известную формулу: \[{\upsilon _{ср}} = \frac{S}{t}\]Здесь \(S\) — весь пройденный путь, \(t\) — всё затраченное время
Первая задача. За четвертую часть времени автомобиль пройдёт \(\frac{1}{4}{\upsilon _1}t\), а за оставшиеся три четверти времени — \(\frac{3}{4}{\upsilon _2}t\). Тогда приведенная выше формула примет вид:\[{\upsilon _{ср}} = \frac{{\frac{1}{4}{\upsilon _1}t + \frac{3}{4}{\upsilon _2}t}}{t} = \frac{1}{4}{\upsilon _1} + \frac{3}{4}{\upsilon _2} = \frac{1}{4} \cdot 20 + \frac{3}{4} \cdot 60 = 50\;км/ч\]
Вторая задача. Одну четвертую часть пути автомобиль проедет за время \({t_1} = \frac{S}{{4{\upsilon _1}}}\), а оставшуюся три четверти пути — за время \({t_2} = \frac{{3S}}{{4{\upsilon _2}}}\). Тогда суммарно автомобиль проедет весь путь за время, равное:\[t = {t_1} + {t_2} = \frac{S}{{4{\upsilon _1}}} + \frac{{3S}}{{4{\upsilon _2}}} = \frac{{S{\upsilon _2} + 3S{\upsilon _1}}}{{4{\upsilon _1}{\upsilon _2}}} = \frac{{S\left( {3{\upsilon _1} + {\upsilon _2}} \right)}}{{4{\upsilon _1}{\upsilon _2}}}\]Тогда приведенная выше формула примет вид:\[{\upsilon _{ср}} = \frac{S}{t} = \frac{S}{{\frac{{S\left( {3{\upsilon _1} + {\upsilon _2}} \right)}}{{4{\upsilon _1}{\upsilon _2}}}}} = \frac{{4{\upsilon _1}{\upsilon _2}}}{{3{\upsilon _1} + {\upsilon _2}}} = \frac{{4 \cdot 20 \cdot 60}}{{3 \cdot 20 + 60}} = 40\;км/ч\]
Два шара с массами 8 и 3 кг двигались навстречу и остановились
после неупругого центрального удара. Определить скорость большего шара до удара, если скорость меньшего шара была 2 м / с.
Совсем же простая задача. Если после столкновения шары остановились (то есть их импульс равен нулю), значит их суммарный импульс изначально был равен нулю по закону сохранения импульса, то есть:\[M\upsilon = mu\]Откуда имеем:\[\upsilon = \frac{{mu}}{M}\]Посчитаем ответ:\[\upsilon = \frac{{2 \cdot 3}}{8} = 0,75\;м/с\]
Мотоциклист проехал половину пути со скоростью 40 км в час.1/6 пути со скоростью 50 км.в час,оставшуюся часть пути со скоростью 80 км.в час.вычислите среднюю скорость
Пусть \(S\) — это весь путь. Половину пути мотоциклист проедет со скоростью \(\upsilon_1\) за время:\[{t_1} = \frac{S}{{2{\upsilon _1}}}\]Шестую часть пути мотоциклист проедет со скоростью \(\upsilon_2\) за время:\[{t_2} = \frac{S}{{6{\upsilon _2}}}\]Оставшуюся часть пути (а осталась треть) мотоциклист проедет со скоростью \(\upsilon_3\) за время:\[{t_3} = \frac{S}{{3{\upsilon _3}}}\]Складываем все время:\[{t_1} + {t_2} + {t_3} = \frac{S}{{2{\upsilon _1}}} + \frac{S}{{6{\upsilon _2}}} + \frac{S}{{3{\upsilon _3}}}\]\[{t_1} + {t_2} + {t_3} = \frac{{3S{\upsilon _2}{\upsilon _3} + S{\upsilon _1}{\upsilon _3} + 2S{\upsilon _1}{\upsilon _2}}}{{6{\upsilon _1}{\upsilon _2}{\upsilon _3}}}\]\[{t_1} + {t_2} + {t_3} = \frac{{S\left( {3{\upsilon _2}{\upsilon _3} + {\upsilon _1}{\upsilon _3} + 2{\upsilon _1}{\upsilon _2}} \right)}}{{6{\upsilon _1}{\upsilon _2}{\upsilon _3}}}\]Среднюю скорость определим так:\[{\upsilon _{ср}} = \frac{S}{{{t_1} + {t_2} + {t_3}}}\]Учитывая вышенаписанное, имеем:\[{\upsilon _{ср}} = \frac{{6{\upsilon _1}{\upsilon _2}{\upsilon _3}S}}{{S\left( {3{\upsilon _2}{\upsilon _3} + {\upsilon _1}{\upsilon _3} + 2{\upsilon _1}{\upsilon _2}} \right)}}\]\[{\upsilon _{11}} = \frac{{6{\upsilon _1}{\upsilon _2}{\upsilon _3}}}{{3{\upsilon _2}{\upsilon _3} + {\upsilon _1}{\upsilon _3} + 2{\upsilon _1}{\upsilon _2}}}\]Считаем численный ответ:\[{\upsilon _{ср}} = \frac{{6 \cdot 40 \cdot 50 \cdot 80}}{{3 \cdot 50 \cdot 80 + 40 \cdot 80 + 2 \cdot 40 \cdot 50}} = 50\;км/ч\]
Здравствуйте, подскажите пожалуйста, если известно только v1 60, v2 40, а найти надо среднюю путевую скорость на первой половине времени. Никак не можем решить. СПАСИБО
Приведите, пожалуйста, полный текст задачи
Здравствуйте. Скажите пожалуйста, а разве ответ не 50 км/ч?
Нет. Доказательство приведено выше. Среднюю скорость нельзя считать просто как среднюю арифметическую скоростей. Иногда, конечно, это «прокатывает», но крайне редко.
Здравствуйте, а откуда в формуле (1/2s+1/2s) / (s/2v1+s/2v2) скорости умножились на 2
Путь поделился пополам, а не скорость умножилась на 2
Я понял
а почему в ответе получается 48 км/ч?
а все я понял. там умножение.
у меня как- то все проще: скорость средняя-это общий путь разделен на общее время. пусть одна половина пути -это S, тогда вторая часть пути тоже s. ищем время первого отрезкак пути и второго- t1=S/v1 b t2 =S/v2. поэтому t1=s/60 b t2 =s/40. считаем общий путь и общее время: общий путь-2S, общее время t= t1+ t2 =s/40+s/60=(слаживаем дроби) 5s/120=s/24. поэтому скорость средняя=2s:s/24=48 (км,час) и переводим
На самом деле Вы проделали то же самое, что и я. Но в Вашем случае есть проблема — если Вас кто-то попросит посчитать значение средней скорости для других значений скоростей автомобиля на участках, то Вам придется проделать все свои действия заново, а мне — нет, поскольку я решил задачу в общем виде. Мне останется только воспользоваться своей формулой и калькулятором.
А откуда 5s ???
\[\frac{S}{{40}} + \frac{S}{{60}} = \frac{{3S + 2S}}{{120}} = \frac{{5S}}{{120}}\]
почему 40+60=120?
Чтобы сложить две дроби, нужно привести их под общий знаменатель. Поищите в интернете информацию как это делать.
Я не пойму откуда взялось 2v +2v
здравствуйте, объясните пожалуйста, не могу понять, как вы выразили знаменатель из вот этой формулы — ?ср=(1/2S+1/2S)/(S/2?1+S/2?2) вот в эту формулу — ?ср=S/((S?2+S?1)/2?1?2) как появились v2 и v1 возле S??
Привел сумму дробей в знаменателе под общий знаменатель:
S/(2*v1)+S/(2*v2)=(S*v2+S*v1)/(2*v1*v2)=S*(v2+v1)/(2*v1*v2)
Так как у нас в знаменателе дроби имеет дробь, то знаменатель последней уходит в числитель, вот и всё.
А, точно, спасибо))) совсем забыл это))
Здравствуйте, не много не понял почему так , t=s/v; у вас t= s1/2v ; но это ведь не правильно, правильно будет t = 1/2s1/v or t = 0.5s1/v ибо если по вашему то общая формула должна быть такой v(ср)= s1+s2/(2s1/2v1 + 2s2/2v2)
У меня t1=S1/v1 и t2=S2/v2, потом я пользуюсь тем, что S1=1/2*S и S2=1/2*S, поэтому t1=S/(2*v1) и t2=S/(2*v2).
Вы в своем сообщении половину индексов потеряли, я вообще ничего не могу в нем понять, так как без индексов смысл весь теряется.
Я уже понял, просто поспешил с комментарием ), но все равно спасибо за ответ.
Задавайте вопросы, всегда рад на них ответить)
а если у нас 1/3 то надо умножать на 3 уже? или так же на 2?
Нет, нужно произвести те же действия, что описаны здесь в ходе решения задачи. Это единственный верный путь.
Зачем переводить в СИ?
Затем, что ответ в задачнике дан в м/с
Уважаемый Модератор, это что за задача???????????
Не понимаю вопроса — Вы имеете ввиду, что она простая?