Решение: Пловец переплывает реку по прямой, перпендикулярной берегу. Определить

Условие задачи:

Пловец переплывает реку по прямой, перпендикулярной берегу. Определить скорость течения, если скорость пловца относительно воды в два раза больше скорости течения. Модуль скорости пловца относительно берега равен 0,5 м/с.

Задача №1.7.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=2 \upsilon_0\), \(\upsilon=0,5\) м/с, \(\upsilon_0-?\)

Решение задачи:

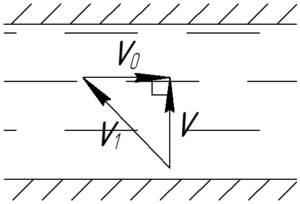Согласно правилу сложения скоростей, вектор скорости пловца относительно берега \(\overrightarrow \upsilon\) – это сумма вектора скорости пловца относительно реки \(\overrightarrow {{\upsilon _1}}\) и вектора скорости течения реки \(\overrightarrow {{\upsilon _0}}\).

\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _1}} + \overrightarrow {{\upsilon _0}} \]

Так как вектор скорости \(\overrightarrow \upsilon\) перпендикулярен берегу, то имеем следующий прямоугольный треугольник (смотри рисунок). Из теоремы Пифагора следует:

\[\upsilon _1^2 = {\upsilon ^2} + \upsilon _0^2\]

По условию \(\upsilon_1=2 \upsilon_0\), поэтому:

\[4\upsilon _0^2 = {\upsilon ^2} + \upsilon _0^2\]

\[3\upsilon _0^2 = {\upsilon ^2} \Rightarrow {\upsilon _0} = \frac{\upsilon }{{\sqrt 3 }}\]

Выполним простой расчет и получим ответ.

\[{\upsilon _0} = \frac{{0,5}}{{\sqrt 3 }} = 0,29\; м/с = 1,04\; км/ч\]