icodepro.ruУсловие задачи:
Поезд первую половину пути шел со скоростью в 1,5 раза большей, чем вторую половину пути. Какова скорость поезда на каждом участке, если средняя скорость прохождения всего пути равна 12 м/с?
Задача №1.2.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=S_2=\frac{1}{2}S\), \(\upsilon_1=1,5\upsilon_2\), \(\upsilon_{ср}=12\) м/с, \(\upsilon_1-?\), \(\upsilon_2-?\)
Решение задачи:
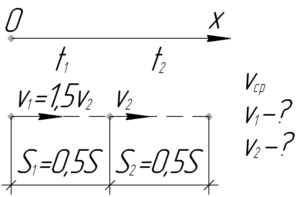В задаче говорится о двух участках пути, которые поезд проходил с разной скоростью. Среднюю скорость на всем пути следует искать по формуле:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Так как движение на обоих участках было равномерное, то время пути \(t_1\) и \(t_2\) найдем из формул:
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Так как по условию \(S_1=S_2=\frac{1}{2}S\) и \(\upsilon_1=1,5\upsilon_2\), то система примет следующий вид:
\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} = \frac{S}{{3{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим выражения в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{3{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}}}} = \frac{S}{{\frac{{5S}}{{6{\upsilon _2}}}}} = \frac{{S \cdot 6{\upsilon _2}}}{{5S}} = \frac{{6{\upsilon _2}}}{5}\]
Значит:
\[{\upsilon _2} = \frac{{5{\upsilon _{ср}}}}{6}\]
\[{\upsilon _1} = 1,5{\upsilon _2} = \frac{3}{2} \cdot \frac{{5{\upsilon _{ср}}}}{6} = \frac{{5{\upsilon _{ср}}}}{4}\]
Теперь сосчитаем ответ.
\[{\upsilon _2} = \frac{{5 \cdot 12}}{6} = 10\; м/с\]
\[{\upsilon _1} = \frac{{5 \cdot 12}}{4} = 15\; м/с\]
Ответ: 15 м/с; 10 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.6 Движение грузового автомобиля описывается уравнением x=-270+12t (м). Когда
1.2.8 С какой постоянной скоростью должна двигаться нефть в трубопроводе с площадью
1.2.9 Катер прошел первую половину пути со скоростью в 2 раза большей, чем вторую
На рисунке изображены два состояния тела, прикреплённого к упругой пружине жёсткостью 500 Н/м: состояние 1-не деформированное состояние физической системы тело – пружина, состояние 2-деформированное состояние которое достигается сжатием пружины под действием F. Определи верные ответы учитывая параметры масштаба оси Ox(x1=10cм). Найти 1) проекцию вектора перемещения тела равна в м
2) Проекция силы упругости действующей на тело равна в Н
я не понимаю, где 4. 3/2 умножается на 5vcp/6, потому что результат 5vcp / 4?
\[\frac{3}{2} \cdot \frac{{5{\upsilon _{ср}}}}{6} = \frac{{15{\upsilon _{ср}}}}{{12}} = \frac{{5{\upsilon _{ср}}}}{4}\]
Если самому поразбираться, то задача лёгкая) Спасибо за помощь
В задаче сказано что средняя скорость 12 м/с, но если найти среднее значение 10 и 15 то получится 12,5. В чем дело?
А с чего вы взяли, что среднее арифметическое этих скоростей должна быть равна средней скорости?
А если поезд шёл со скоростью 15 м/с?
Если условие Вашей задачи отличается только численным значением скорости, то используйся общее решение, приведенное в условии. Если нет, то мне нужно полное условие, иначе я не смогу решить.
ответьте пожалуйста. когда подставляли выражения в \(\upsilon_{ср}\) откуда взялось \(5S\)?
В знаменателе имеем сумму двух дробей, чтобы их сложить, нужно привести их под общий знаменатель. Показываю:
$$\frac{S}{{3{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}} = \frac{{2S}}{{6{\upsilon _2}}} + \frac{{3S}}{{6{\upsilon _2}}} = \frac{{2S + 3S}}{{6{\upsilon _2}}} = \frac{{5S}}{{6{\upsilon _2}}}$$
Так как эта дробь находится в знаменателе другой дроби, то её знаменатель (т.е. \({6{\upsilon _2}}\)) уйдёт в числитель другой дроби.
Извините, а откуда взялось 3v(1) + 2v(2)
Смотрите, так как движение на обоих участках равномерное, то время\(t_1\) и \(t_2\) найдем из формул:\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]Так как по условию \({S_1} = {S_2} = \frac{S}{2}\), то (я сейчас заменяю \(S_1\) и \(S_2\) на \(\frac{S}{2}\)):\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]Также по условию \({\upsilon _1} = 1,5{\upsilon _2}\), поэтому (вместо \(\upsilon_1\) подставляю \(1,5\upsilon_2\)):\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2 \cdot 1,5{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]Окончательно имеем:\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{3{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Как получилось,что t1=S/2v1=S/3v2 и t2=S/2v2 ,объясните,пожалуйста.Не понимаю.
Время t1, за которое поезд прошел первую половину пути, очевидно, можно найти по формуле:
t1=S/2v1 (т.е. я половину пути S/2 разделил на скорость v1)
Так как по условию v1=1,5v2, то формула примет такой вид:
t1=S/3v2
Аналогично, время t2, за которое поезд прошел вторую половину пути, можно найти по формуле:
t2=S/2v2 (т.е. я половину пути S/2 разделил на скорость v2)
Поняла все,кроме этого :”Так как по условию v1=1,5v2, то формула примет такой вид:
t1=S/3v2″ . Как получилась тройка в знаменателе,объясните,пожалуйста.
Ну у вас в знаменателе 2v1. Так как v1=1,5v2, то 2*v1=2*1,5v2=3v2.
С этой задачей все ясно, спасибо. Помогите решить такую задачу:
Два бегуна стартовали с разными скоростями. 1-й из них пробежал всю дистанцию с постоянной скоростью. 2-й первую часть дистанции пробежал со скоростью в к раз выше, чем 1-й, зато вторую часть со скоростью в к раз меньше чем 1-й. Однако финиша они достигли одновременно. Определить соотношение первой части дистанции ( на которой 2-й бегун двигался быстрее) ко всей дистанции.
Напишите в нашу группу ВК, я там отвечу
меня нет в контакте