Условие задачи:
Пуля, летящая со скоростью 141 м/с, попадает в доску и проникает на глубину 6 см. Определить скорость пули на глубине 3 см, если пуля в доске двигалась равнозамедленно.
Задача №1.3.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=141\) м/с, \(L=6\) см, \(l=3\) см, \(\upsilon_1-?\)
Решение задачи:
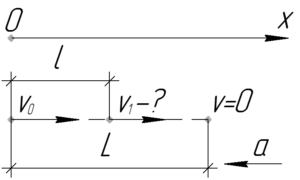 Запишем систему из двух уравнений: первая – для всего пути \(L\), вторая – для пути \(l\), используя известную формулу кинематики без времени.
Запишем систему из двух уравнений: первая – для всего пути \(L\), вторая – для пути \(l\), используя известную формулу кинематики без времени.
\[\left\{ \begin{gathered}
{\upsilon ^2} – \upsilon _0^2 = – 2aL \hfill \\
\upsilon _1^2 – \upsilon _0^2 = – 2al \hfill \\
\end{gathered} \right.\]
Понятно, что в конце пути тело остановится, поэтому \(\upsilon=0\). В итоге система примет вид:
\[\left\{ \begin{gathered}
\upsilon _0^2 = 2aL \;\;\;\;(1)\hfill \\
\upsilon _0^2 – \upsilon _1^2 = 2al \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Поскольку мы не знаем ускорения \(a\), то поделим уравнение (2) на уравнение (1).
\[\frac{{\upsilon _0^2 – \upsilon _1^2}}{{\upsilon _0^2}} = \frac{l}{L}\]
Остается только выразить скорость \(\upsilon_1\), для чего перемножим равенство крест-накрест и перенесем все члены с \(\upsilon_1\) в одну часть.
\[L\upsilon _0^2 – L\upsilon _1^2 = l\upsilon _0^2\]
\[L\upsilon _1^2 = \upsilon _0^2\left( {L – l} \right)\]
\[{\upsilon _1} = {\upsilon _0}\sqrt {\frac{{L – l}}{L}} \]
Подставим числа в формулу, не забыв перевести их в единицы системы СИ.
\[{\upsilon _1} = 141\sqrt {\frac{{0,06 – 0,03}}{{0,06}}} = 99,7\; м/с \approx 100\; м/с\]
Ответ: 100 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.48 Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти
1.3.50 Пробежав с постоянным ускорением по взлетной полосе 750 м, самолет
1.3.51 Поезд метрополитена разгоняется от остановки с постоянным ускорением

 icodepro.ru
icodepro.ru
Куда ушёл минус в 1 уравнении
А где минус у 2al?
Если \(\upsilon = 0\), то уравнение (1) примет вид:\[ – \upsilon _0^2 = – 2aL\]Или, что то же самое: \[\upsilon _0^2 = 2aL\]В уравнении (2) пропал знак “минус”, потому что мы переставили местами квадраты скоростей.
Почему поделим уравнение (2) на уравнение (1), а не наоборот??
Не имеет разницы, можете делить наоборот
почему -2аL???????
Потому что движение равнозамедленное, а в левой части равенства я пишу разность квадратов конечной и начальной скоростей.