Условие задачи:
 Шкив радиусом 10 см приводится во вращение грузом, подвешенным на нити. Груз опускается с ускорением 2 см/с2. Какова угловая скорость шкива в тот момент, когда груз пройдет путь 1 м? (Рисунок, данный к условию задачи, приведен справа.)
Шкив радиусом 10 см приводится во вращение грузом, подвешенным на нити. Груз опускается с ускорением 2 см/с2. Какова угловая скорость шкива в тот момент, когда груз пройдет путь 1 м? (Рисунок, данный к условию задачи, приведен справа.)
Задача №1.8.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=10\) см, \(a=2\) см/с2, \(L=1\) м, \(\omega-?\)
Решение задачи:
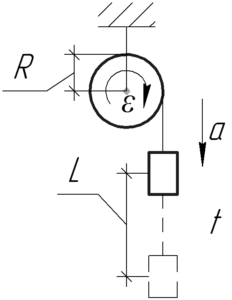 Груз опускается равноускоренно — так как груз связан со шкивом посредством нерастяжимой нити, значит, каждая точка шкива будет такое же линейное ускорение \(a\). Таким образом, мы имеем дело с равноускоренным вращением шкива, значит, у всех точек имеется также и угловое ускорение \(\varepsilon\). Его можно найти, зная формулу связи:
Груз опускается равноускоренно — так как груз связан со шкивом посредством нерастяжимой нити, значит, каждая точка шкива будет такое же линейное ускорение \(a\). Таким образом, мы имеем дело с равноускоренным вращением шкива, значит, у всех точек имеется также и угловое ускорение \(\varepsilon\). Его можно найти, зная формулу связи:
\[a = \varepsilon R \Rightarrow \varepsilon = \frac{a}{R}\;\;\;\;(1)\]
При равноускоренном вращении шкива угловая скорость \(\omega\) нарастает линейно со временем.
\[\omega = \varepsilon t\;\;\;\;(2)\]
Осталось только найти время \(t\). Так как груз движется равноускоренно без начальной скорости, то:
\[L = \frac{{a{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2L}}{a}}\;\;\;\;(3)\]
Подставим выражения (1) и (3) в (2) и получим ответ в общем виде.
\[\omega = \frac{a}{R}\sqrt {\frac{{2L}}{a}} = \frac{{\sqrt {2aL} }}{R}\]
Переведем радиус и ускорение в систему СИ.
\[10\; см = \frac{{10}}{{100}}\; м = 0,1\; м\]
\[2\; см/с^2 = \frac{2}{{100}}\; м/с^2 = 0,02\; м/с^2\]
Численно ответ равен:
\[\omega = \frac{{\sqrt {2 \cdot 0,02 \cdot 1} }}{{0,1}} = 2\; рад/с\]
Ответ: 2 рад/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.24 Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов
1.8.26 Определить радиус колеса, если при вращении скорость точек на ободе колеса
1.8.27 Для того чтобы повернуть трактор, движущийся со скоростью 18 км/ч, тракторист

 icodepro.ru
icodepro.ru
Почему гравитацию не учли?
УТОЧНЕНИЕ!!!
Груз опускается ИЗ СОСТОЯНИЯ ПОКОЯ с ускорением…