Решение: Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени

Условие задачи:

Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени 1 с между двумя моментами, когда тело находится на высоте 10 м. Найти начальную скорость тела.

Задача №1.4.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\Delta t=1\) с, \(h=10\) м, \(\upsilon_0-?\)

Решение задачи:

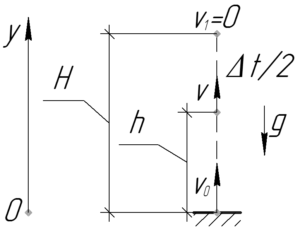На сайте уже есть подобная решенная задача, поэтому эту задачу будет полезно решить тем, кто уже знаком с указанной. Решается она таким же образом (рисунок к задаче вообще совпадает полностью), и для начала запишем следующую формулу:

\[{\upsilon_1 ^2} – \upsilon _0^2 = – 2gH\]

В этой формуле: \(\upsilon_0\) – скорость тела при броске; \(\upsilon_1\) – скорость в наивысшей точке полета, которая, естественно, равна нулю; \(H\) – максимальная высота, на которую поднимется тело, ее не нужно путать с высотой \(h\), данной в условии. Значит:

\[\upsilon _0^2 = 2gH\]

\[{\upsilon _0} = \sqrt {2gH} \]

Нам неизвестна высота \(H\). Чтобы ее узнать, необходимо знать:

скорость тела \(\upsilon\) на высоте \(h\);
время полета тела от высоты \(h\) до высоты \(H\).

На самом деле ответ на второй вопрос прост – это \(\frac{\Delta t}{2}\). Это исходит из аналогии тому факту, что время подъема тела до максимальной высоты и время падения с этой высоты одинаково. Но зная это время, мы можем найти ответ на первый вопрос, поскольку тело движется равнозамедленно с ускорением \(g\):

\[0 = \upsilon – g\frac{{\Delta t}}{2} \Rightarrow \upsilon = g\frac{{\Delta t}}{2}\]

Теперь запишем уравнения движения тела в общем виде.

\[oy:y = h + \upsilon t – \frac{{g{t^2}}}{2}\]

Для момента времени \(t=\frac{\Delta t}{2}\) координата \(y\) станет равной высоте \(H\). Учитывая, что \(\upsilon=g\frac{{\Delta t}}{2}\), имеем:

\[H = h + g\frac{{\Delta t}}{2}\frac{{\Delta t}}{2} – \frac{g}{2}\frac{{\Delta {t^2}}}{4} = h + \frac{{g\Delta {t^2}}}{8}\]

Окончательная формула для получения ответа в общем виде показана ниже:

\[{\upsilon _0} = \sqrt {2g\left( {h + \frac{{g\Delta {t^2}}}{8}} \right)} \]

\[{\upsilon _0} = \sqrt {2 \cdot 10\left( {10 + \frac{{10 \cdot {1^2}}}{8}} \right)} = 15\; м/с \]