Тело брошено горизонтально с высоты h=20 м. Траектория его движения

Условие задачи:

Тело брошено горизонтально с высоты \(h=20\) м. Траектория его движения описывается уравнением \(y=20-0,05x^2\). Найти скорость, с которой было брошено тело.

Задача №1.5.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=20\) м, \(y=20-0,05x^2\), \(\upsilon_0-?\)

Решение задачи:

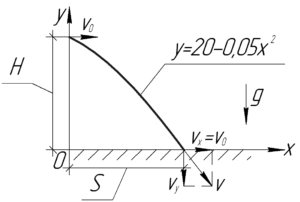Посмотрите на рисунок к задаче, который мы привели справа. Видно, что когда тело достигнет земли, то его координата \(y\) станет равной нулю, поэтому воспользуемся уравнением траектории и найдем координату \(x\), соответствующую этому моменту времени.

\[\left\{ \begin{gathered}
y = 20 – 0,05{x^2} \hfill \\
y = 0 \hfill \\
\end{gathered} \right. \Rightarrow 20 – 0,05{x^2} = 0\]

Решим это квадратное уравнение.

\[0,05{x^2} = 20\]

\[{x^2} = 400\]

\[\left[ \begin{gathered}
x = 20 \hfill \\
x = – 20 \hfill \\
\end{gathered} \right.\]

Отбросим отрицательный корень, поскольку тело бросалось в положительном направлении оси \(x\).

Теперь запишем уравнения движения в проекциях на ось \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:x = {\upsilon _0}t\,\,\,\,\,\,(1) \hfill \\
oy:y = \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]

Если в уравнениях (1) и (2) переменная \(t\) станет равной времени падения, то будет справедливо записать:

\[\left\{ \begin{gathered}
S = {\upsilon _0}t\,\,\,\,\,\,(3) \hfill \\
H = \frac{{g{t^2}}}{2}\,\,\,(4) \hfill \\
\end{gathered} \right.\]

Причем дальность полета \(S\) мы нашли, решив квадратное уравнение, значит, \(S=20\) м.

Далее найдем время падения \(t\) из выражения (4).

\[t = \sqrt {\frac{{2H}}{g}} \]

Из формулы (3) выразим искомую начальную скорость \(\upsilon_0\) и в полученное выражение подставим формулу для времени.

\[{\upsilon _0} = \frac{S}{t} = S\sqrt {\frac{g}{{2H}}} \]

Сосчитаем численный ответ:

\[{\upsilon _0} = 20\sqrt {\frac{{10}}{{2 \cdot 20}}}  = 10\; м/с \]

Ответ: 10 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.5.10 Спортсменка, стоящая на вышке, бросает мяч с горизонтальной скоростью
1.6.1 Тело брошено со скоростью 10 м/с под углом 30 градусов к горизонту
1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска