icodepro.ruУсловие задачи:
Тело брошено со скоростью 10 м/с под углом 30° к горизонту. Через какое время оно будет на высоте 1,05 м?
Задача №1.6.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(v_0=10\) м/с, \(\alpha=30^\circ\), \(h=1,05\) м, \(t-?\)
Решение задачи:
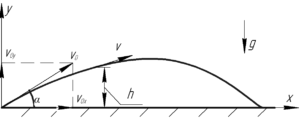Задача очень простая, на умение записывать уравнения движения тел в соответствующих осях. Рисунок для решения мы приводим справа, для его увеличения нажмите на него.
Запишем уравнения движения тела по оси \(y\):
\[y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\]
Заменяя в уравнении \(y\) на данное \(h\), получим квадратное уравнения, которое необходимо решить для нахождения времени полета. Неудивительно, что уравнение имеет 2 корня, поскольку на данной высоте тело за все время полета будет находиться 2 раза, что видно из рисунка.
\[h = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\]
\[g{t^2} – 2{v_0}\sin \alpha \cdot t + 2h = 0\]
Найдем дискриминант:
\[D = 4v_0^2{\sin ^2}\alpha – 8gh\]
Проверять положительность дискриминанта не будем, поскольку решение задачи быть должно, значит он априори неотрицателен.
Тогда корни квадратного уравнения равны:
\[t = \frac{{2{v_0}\sin \alpha \pm \sqrt {4v_0^2{{\sin }^2}\alpha – 8gh} }}{{2g}}\]
Мы получили ответ в общем виде. Теперь подставим все известные величины в СИ:
\[t = \frac{{2 \cdot 10 \cdot \sin 30^\circ \pm \sqrt {4 \cdot {{10}^2} \cdot {{\sin }^2}30^\circ – 8 \cdot 10 \cdot 1,05} }}{{2 \cdot 10}}\]
Получаем два корня:
\[\left[ \begin{gathered}
t = 0,7 \; с \hfill \\
t = 0,3 \; с \hfill \\
\end{gathered} \right.\]
Вероятнее всего, автор имел в виду первое нахождение на этой высоте.
Ответ: 0,3 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.5.11 Тело брошено горизонтально с высоты h=20 м. Траектория его движения
1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска
1.6.3 Камень, брошенный с земли под углом 45 градусов к горизонту
Куда делся t в уравнении дискриминанта?
А \(t\) там и не должно быть, поскольку мы решаем это квадратное уравнение относительно \(t\).
Из математики известно, что для решения уравнения вида \(a{x^2} + bx + c = 0\) (относительно \(x\)) нам нужно определить дискриминант \(D\), который определяется так:\[D = {b^2} – 4ac\]Как Вы и сами видите, в выражении для дискриминанта \(x\) отсутствует (что и не удивительно, поскольку \(x\) – это искомая неизвестная).
Верно, спасибо
Можно ли было решить эту задачу, используя формулу t = V0 * sin? / g?
Конечно нет, поскольку Ваша формула используется для нахождения времени, за которое тело достигнет наивысшей точки траектории своего движения.
С чего Вы взяли, за время \(t\), данное в условии, тело достигнет именно этой точки, а не любой другой?
Почему нельзя просто выразить t из уравнения?
В случае квадратного уравнения выразить не получится, попробуйте сами, здесь нужно решать.
Почему синус?
Потому что проекция скорости на ось y выражается через синус. Можете сами в этом убедиться, спроецировав этот вектор и посмотрев на получившийся прямоугольный треугольник из векторов.
t=0,3с – это первое время когда тело будет на расстоянии 1,05м
t=0,7с – это время когда тело будет падать обратно на землю, оно так же будет 1,05м
Это понятно, просто в ответах в сборнике к этой задаче указан один корень – первый (t=0,3 с), значит автор имел ввиду первое нахождение тела на указанной высоте.