icodepro.ruУсловие задачи:
Тело бросили под углом 60° к горизонту со скоростью 10 м/с. Определить момент времени, когда скорость будет направлена под углом 45° к горизонту.
Задача №1.6.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(v_0=10\) м/с, \(\beta=45^\circ\), \(t-?\)
Решение задачи:
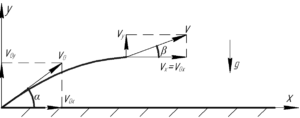Для понимания решения данной задачи воспользуйтесь рисунком. Кстати, мы уже приводили решение подобной задачи. Т.к. вектор скорости тела составит с горизонтом угол 45°, то составляющие вектора скорости (т.е. его проекции на ось \(x\) и \(y\)) равны, поскольку в прямоугольном треугольнике с углом 45° равны катеты.
Запишем уравнения скорости в проекциях на оси:
\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt \hfill \\
\end{gathered} \right.\]
Условие равенства составляющих запишется следующим образом:
\[{v_0}\sin \alpha – gt = {v_0}\cos \alpha \]
Отсюда и найдем искомое время:
\[t = \frac{{{v_0}\left( {\sin \alpha – \cos \alpha } \right)}}{g}\]
Подставим все известные величины в системе измерения СИ и найдем ответ численно:
\[t = \frac{{10\left( {\sin 60^\circ – \cos 60^\circ } \right)}}{{10}} = 0,37\; с.\]
Ответ: 0,37 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.10 Снаряд вылетает из орудия со скоростью 1000 м/с под углом 60
1.6.12 Тело брошено с начальной скоростью 40 м/с под углом 30 градусов
1.6.13 Бомбардировщик пикирует на цель под углом 60 градусов к горизонту
А почему тогда Vy равен Vosina-gt а не Vosinb-gt? Ведь угол же поменялся
Скорость тела, брошенного под углом к горизонту, в любой момент времени можно найти с помощью следующего векторного уравнения:\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _0}} + \overrightarrow g t\]Это векторное уравнение можно перевести в два алгебраических путем проецирования векторов, входящих в векторное уравнение, на оси координат. Получим:\[\left\{ \begin{gathered}
{\upsilon _x} = {\upsilon _0}\cos \alpha \hfill \\
{\upsilon _y} = {\upsilon _0}\sin \alpha – gt \hfill \\
\end{gathered} \right.\]Проекции вектора начальной скорости никак изменяться не могут (слагаемые в уравнениях с \(\upsilon_0\) и есть проекции начальной скорости на соответствующие оси координат).
При таких условиях вектор скорости составит угол 45° с горизонтом дважды? Если так то как можно найти t2?
Ничего не понял
Просто в подобной задаче ответа 2 а не 1. К примеру ответы к моей задаче 0.73 и 2.73. Как найти 0.73 я понял,а как получилось 2.73 нет.
Все получилось. Оказалось что нужно было рассматривать 2 движения: Тело брошено вертикально со скоростью и Тело брошено вниз со скоростью. В итоге для Vy получилось 2 уравнения Vy=-V0y+gt-падает вниз и Vy=V0y-gt-поднимается вверх
А, это Вы верно заметили, что в задаче два верных ответа, спасибо! Думаю Ваш комментарий многим окажется полезен.
почему v0sin?—gt=v0cos?
Т.к. вектор скорости тела в момент времени t составит с горизонтом угол 45°, то составляющие вектора скорости (то есть его проекции на ось x и y) равны, поскольку в прямоугольном треугольнике с углом 45° катеты равны.