icodepro.ruУсловие задачи:
Тело, двигаясь с места равноускоренно, проходит за четвертую секунду от начала движения 7 м. Какой скорости оно достигнет в конце десятой секунды?
Задача №1.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_4=7\) м, \(\upsilon_{10}-?\)
Решение задачи:
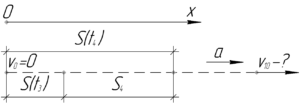В общем виде уравнение равноускоренного движения тела выглядит так:
\[S\left( t \right) = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]
Тело двигалось с места, значит его начальная скорость \(\upsilon_0\) равна нулю.
\[{\upsilon _0} = 0\]
Значит уравнение движения сводится к более простой форме:
\[S\left( t \right) = \frac{{a{t^2}}}{2}\;\;\;\;(1)\]
Путь за четвертую секунду \(S_4\) найдем как разность пути за \(t_4=4\) секунды и пути за \(t_3=3\) секунды.
\[{S_4} = S\left( t_4 \right) – S\left( t_3 \right)\]
Используя уравнение (1), имеем:
\[{S_4} = \frac{{at_4^2}}{2} – \frac{{at_3^2}}{2} = \frac{{a\left( {t_4^2 – t_3^2} \right)}}{2}\]
Выразим неизвестное ускорение \(a\):
\[a = \frac{{2{S_4}}}{{t_4^2 – t_3^2}}\]
Чтобы ответить на вопрос задачи, запишем формулу скорости для равноускоренного движения:
\[\upsilon = {\upsilon _0} + at\]
Учтем, что \(\upsilon_0=0\), поэтому скорость тела к концу 10-й секунды можно найти по такой формуле:
\[{\upsilon _{10}} = a{t_{10}}\]
Подставим в формулу полученное нами ранее выражение для ускорения \(a\) и будем иметь окончательную формулу:
\[{\upsilon _{10}} = \frac{{2{S_4}{t_{10}}}}{{t_4^2 – t_3^2}}\]
Подставив численные данные задачи, сосчитаем ответ:
\[{\upsilon _{10}} = \frac{{2 \cdot 7 \cdot 10}}{{{4^2} – {3^2}}} = 20\; м/с = 72\; км/ч\]
Ответ: 72 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.37 Тело движется с начальной скоростью 4 м/с вдоль прямой, причем его скорость
1.3.39 Тело, имея некоторую начальную скорость, движется равноускоренно. За время
1.3.40 Точка движется равноускоренно. За 4 с она проходит путь 24 м. За следующие
