Тело движется равномерно по окружности. Во сколько раз увеличится

Условие задачи:

Тело движется равномерно по окружности. Во сколько раз увеличится центростремительное ускорение тела, если скорость увеличить в два раза, а радиус окружности уменьшить в 4 раза?

Задача №1.8.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_2=2\upsilon_1\), \(R_2=\frac{R_1}{4}\), \(\frac{a_{ц2}}{a_{ц1}}-?\)

Решение задачи:

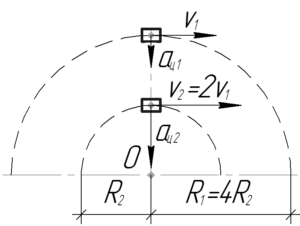При равномерном движении тела со скоростью \(\upsilon\) по окружности радиуса \(R\) его центростремительное ускорение можно найти по формуле:

\[a_ц = \frac{{{\upsilon ^2}}}{R}\]

Найдем во сколько раз изменится это ускорение при изменении скорости и радиуса окружности:

\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{\upsilon _2^2 \cdot {R_1}}}{{{R_2} \cdot \upsilon _1^2}}\]

Так как скорость увеличилась в 2 раза, а радиус уменьшился в 4 раза, то:

\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{4\upsilon _1^2 \cdot {R_1}}}{{\frac{{{R_1}}}{4} \cdot \upsilon _1^2}} = 4 \cdot 4 = 16\]

Ответ: увеличится в 16 раз.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.11 Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз
1.8.13 Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с-1. Определить
1.8.14 Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его