Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его

Условие задачи:

Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его колеса, если их радиус 50 см?

Задача №1.8.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=60\) км/ч, \(R=50\) см, \(\nu-?\)

Решение задачи:

По сути в задаче спрашивают частоту вращения колеса, которое и показывает количество оборотов в секунду.

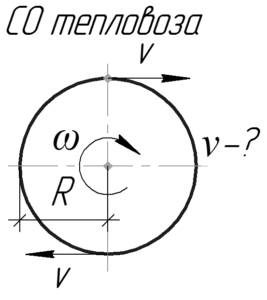
Как уже много раз говорилось в решениях задач на этом сайте, строго говоря, колеса совершают только вращательное движение в системе отсчета (СО), связанной с самим тепловозом. В системе отсчета Земли (т.е. для стороннего наблюдателя) колеса совершают так называемое качение, которое является совокупностью поступательного и вращательного движения. Характерно, что при качении колеса тепловоза без проскальзывания точка соприкосновения с рельсами не имеет скорости (только относительно Земли!). Будет очень здорово, если Вы запомните этот факт.

В СО тепловоза линейная скорость крайних точек колеса равна скорости тепловоза, с которой он движется относительно Земли. Связь линейной и угловой скорости выглядит так:

\[\upsilon  = \omega R \Rightarrow \omega  = \frac{\upsilon }{R}\]

Частота вращения связана с угловой скоростью соотношением:

\[\omega  = 2\pi \nu  \Rightarrow \nu  = \frac{\omega }{{2\pi }}\]

Подставим первую формулу во вторую, чтобы получить ответ в общем виде.

\[\nu  = \frac{\upsilon }{{2\pi R}}\]

Переведем численные данные задачи в систему СИ.

\[60\; км/ч = \frac{{60 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{600}}{{36}}\; м/с = \frac{{50}}{3}\; м/с\]

\[50\; см = \frac{{50}}{{100}}\; м = 0,5\; м\]

В итоге:

\[\nu  = \frac{{50}}{{3 \cdot 2 \cdot 3,14 \cdot 0,5}} = 5,31\; [1/с]\]

Ответ: 5,31 [1/с].

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.13 Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с-1. Определить
1.8.15 К валу, радиус которого 5 см, прикреплена нить. Через 5 с после начала равномерного
1.8.16 Велосипедист начинает двигаться делать поворот по кругу со скоростью 10 м/с