icodepro.ruУсловие задачи:
У светофора трактор, движущийся равномерно со скоростью 18 км/ч, обогнал автомобиль, который из состояния покоя начал двигаться с ускорением 1,25 м/с2. Определить, на каком расстоянии от светофора автомобиль обгонит трактор.
Задача №1.3.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=18\) км/ч, \(a_2=1,25\) м/с2, \(S-?\)
Решение задачи:
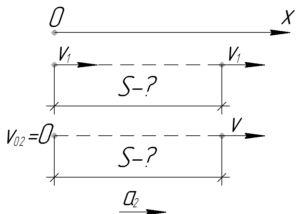Запишем уравнения движения трактора и автомобиля вдоль оси \(x\).
\[\left\{ \begin{gathered}
x = {\upsilon _1}t \hfill \\
x = \frac{{{a_2}{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Верхнее уравнение – это уравнение равномерного движения трактора, второе – уравнение равноускоренного движения автомобиля без начальной скорости.
Когда автомобиль начнет обгонять трактор, то их координаты станут равны между собой. Приравняв уравнения, найдем момент времени \(t\), когда это произойдет.
\[{\upsilon _1}t = \frac{{{a_2}{t^2}}}{2}\]
\[\frac{{{a_2}{t^2}}}{2} – {\upsilon _1}t = 0\]
\[t\left( {\frac{{{a_2}t}}{2} – {\upsilon _1}} \right) = 0\]
Получаем два корня, первый из которых соответствует моменту встречи у светофора (\(t=0\)), а второй корень – уже второй встрече (извините за тавтологию) данных тел.
\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{\upsilon _1}}}{{{a_2}}} \hfill \\
\end{gathered} \right.\]
Подставим второй корень в любое из уравнений движения и получим ответ на вопрос задачи.
\[S = {\upsilon _1}\frac{{2{\upsilon _1}}}{{{a_2}}} = \frac{{2\upsilon _1^2}}{{{a_2}}}\]
Подставив данные задачи в выражение, сосчитаем ответ, но сперва переведем значение \(\upsilon_1\) из км/ч в м/с.
\[18\; км/ч = \frac{{18 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{180}}{{36}}\; м/с = 5\; м/с \]
\[S = \frac{{2 \cdot {5^2}}}{{1,25}} = 40\; м \]
Ответ: 40 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.26 Скорость движения тела, равная 10 м/с, за 17 с уменьшилась в 5 раз. Определить
1.3.28 Автомобиль двигался со скоростью 4 м/с, затем был выключен двигатель
1.3.29 Автомобиль начал двигаться с ускорением 1,5 м/с2 и через некоторое время
есть похожая задача\ автомобиль Б движется со скоростью 20 м/с и обгоняет автомобиль А ,движущийся со скоростью 15м/с. Через 10 секунд автомобиль А начал двигаться с ускорением 2 м/с2 и держал это ускорение пока не обогнал автомобиль Б.
Вопрос/ какой промежуток времени между двумя обгонами?
Отсчет времени будем вести с момента первого обгона. Пусть второй обгон совершится через искомое время \(t\), тогда автомобиль Б пройдет путь \({\upsilon _1}t\), а автомобиль А – \({\upsilon _2}t + \frac{{a{{\left( {t – \tau } \right)}^2}}}{2}\). Здесь \(\tau\) – время, после которого автомобиль А начнет ускоряться, то есть \(\tau = 10\) с. Понятно, что автомобили прошли одинаковый путь, поэтому для решения задачи нужно решить следующее квадратное уравнение:\[{\upsilon _1}t = {\upsilon _2}t + \frac{{a{{\left( {t – \tau } \right)}^2}}}{2}\]Подставим численные значения величин из условия:\[20t = 15t + \frac{{2{{\left( {t – 10} \right)}^2}}}{2}\]\[5t = {\left( {t – 10} \right)^2}\]\[5t = {t^2} – 20t + 100\]\[{t^2} – 25t + 100 = 0\]\[D = {25^2} – 4 \cdot 100 = 225 = {15^2}\]\[t = \frac{{25 \pm 15}}{2}\]\[\left[ \begin{gathered}
t = 20 \hfill \\
t = 5 \hfill \\
\end{gathered} \right.\]Второй корень не может быть решением задачи, поскольку автомобиль А начнет ускорение через 10 с после первого обгона, т.е. второй обгон не может произойти раньше, чем через 10 с после первого.
Здравствуйте. К задаче (автомобиль Б движется со скоростью 20 м/с) для полного понимания ещё рисунок, уравнения в векторной форме и в проекциях на оси координат нужны.
А второй вопрос: откуда пришло понимание, что автомобили прошли одинаковый путь (А прошёл 150 м, за 10 с, а Б прошёл 200 м за эти же 10 с, затем А ускорился (2 м/с2, то есть за 11-ю с 157 м и далее 157+19(12-я с)+21+23+25+27+29+31+33+35(20-я секунда: А только догнал Б)=400 м , а на 21 секунде А проехал 422 м, Б 420 м.
Третий вопрос: то есть промежуток времени между двумя обгонами это промежуток времени, в течение которого не было обгона, то есть 20 секунд?
К сожалению, нет возможности прикреплять рисунок в комментариях. Уравнения движения:\[\left\{ \begin{gathered}
\overrightarrow {{x_1}} = \overrightarrow {{\upsilon _1}} t \hfill \\
\overrightarrow {{x_2}} = \overrightarrow {{\upsilon _2}} \tau + \overrightarrow {{\upsilon _2}} \left( {t – \tau } \right) + \frac{{\overrightarrow a {{\left( {t – \tau } \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]Автомобили прошли одинаковый путь, потому что они начали совершать обгон. Учитывая ненулевую и увеличивающуюся относительную скорость автомобиля А (относительно автомобиля Б) в момент обгона, факт начала обгона есть подтверждение дальнейшего полного обгона. Не знаю к чему Ваши вопросы, в задаче подразумевается, что автомобили – материальные точки.
Третий вопрос – да.
как вы получили второй корень я не понял немного можете подробнее
там я знаменатель привел на 2 там входит a_2*t_2*2u_1/2
Всё элементарно. У меня есть такое уравнение:
\(\frac{{{a_2}{t^2}}}{2} – {\upsilon _1}t = 0\)
Выношу за скобки время \(t\):
\(t\left( {\frac{{{a_2}t}}{2} – {\upsilon _1}} \right) = 0\)
Как видите, мы получили произведение времени \(t\) на скобку. Когда произведение равно нулю? Правильно, когда либо первый, либо второй множитель равен нулю, поэтому:
\(\left[ \begin{gathered}
t = 0 \hfill \\
\frac{{{a_2}t}}{2} – {\upsilon _1} = 0 \hfill \\
\end{gathered} \right.\)
Ну и окончательно получаем:
\(\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{\upsilon _1}}}{{{a_2}}} \hfill \\
\end{gathered} \right.\)
Спасибо большое
я думаю, что там должен быть знак больше 40 м
Почему?
Обгон это же вроде, если машина проехала так, что конец одной совпал с началом другой, поэтому больше 40 м, но тут нету такого.
В данном случае трактор и автомобиль рассматриваем как материальные точки. Нет особого смысла рассматривать их как объекты, имеющие длины, от этого ничего не изменится.
Спасибо этому сайту. Стал немного понимать физику. Отдельное спасибо Easyfizika за ответы в комментариях.