Условие задачи:
Упругий шар, падая с высоты 80 м, после удара о Землю, отскакивает вертикально вверх со скоростью 0,75 скорости его при падении. Сколько времени пройдет от начала движения шара до второго удара о Землю?
Задача №1.4.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=80\) м, \(\upsilon_0=0,75 \upsilon\), \(t-?\)
Решение задачи:
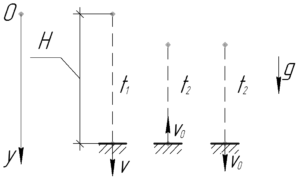 Искомое время можно найти по формуле:
Искомое время можно найти по формуле:
\[t = {t_1} + 2{t_2}\]
Здесь \(t_1\) – время падения шара с высоты \(H\), \(t_2\) – время подъема шара после соударения с Землей и время падения с некоторой после подъема, поскольку эти длительности равны.
Шар падал без начальной скорости, поэтому определить время \(t_1\) не составит трудности. Для этого воспользуемся знакомой всем формулой:
\[H = \frac{{gt_1^2}}{2} \Rightarrow {t_1} = \sqrt {\frac{{2H}}{g}} \]
При этом шар в момент касания земли будет иметь скорость:
\[\upsilon = g{t_1}\]
\[\upsilon = g\sqrt {\frac{{2H}}{g}} = \sqrt {2gH} \]
После удара о Землю шар потеряет некоторую часть скорости (точнее энергию) и начнет подниматься. В точке наивысшего подъема его скорость будет равна нулю, из этих соображений найдем время \(t_2\).
\[0 = {\upsilon _0} – g{t_2} \Rightarrow {t_2} = \frac{{{\upsilon _0}}}{g}\]
Так как \(\upsilon_0=0,75 \upsilon\) и \(\upsilon = \sqrt {2gH} \), значит:
\[{t_2} = \frac{{0,75\upsilon }}{g} = \frac{{3\upsilon }}{{4g}} = \frac{{3\sqrt {2gH} }}{{4g}} = \frac{3}{4}\sqrt {\frac{{2H}}{g}} \]
В итоге, подставим все выражения в самую первую формулу, получим:
\[t = \sqrt {\frac{{2H}}{g}} + 2 \cdot \frac{3}{4}\sqrt {\frac{{2H}}{g}} \]
\[t = \frac{5}{2}\sqrt {\frac{{2H}}{g}} \]
Сосчитаем ответ.
\[t = \frac{5}{2}\sqrt {\frac{{2 \cdot 80}}{{10}}} = 10\; с \]
Ответ: 10 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.46 Тело свободно падает с высоты 5 м. Найти среднюю скорость тела на нижней
1.4.48 Цепочка шаров висит над поверхностью стола: первый шар – на высоте 1 м, второй
1.4.49 Свободно падающее без начальной скорости тело пролетело мимо точки A

 icodepro.ru
icodepro.ru