Условие задачи:
В момент, когда тронулся поезд, провожающий стал равномерно бежать по ходу поезда со скоростью 3,5 м/с. Принимая движение поезда равноускоренным, определить скорость поезда в тот момент, когда уезжающий поравняется с провожающим.
Задача №1.7.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_2=3,5\) м/с, \(\upsilon_1-?\)
Решение задачи:
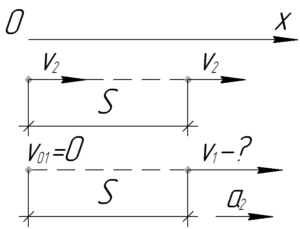 Провожающий пройдет такое же расстояние, как и уезжающий, относительно Земли, когда они поравняются друг с другом. Так как первый шел равномерно, а поезд (вместе с уезжающим) двигался равноускоренно, то запишем их уравнения движения в системе:
Провожающий пройдет такое же расстояние, как и уезжающий, относительно Земли, когда они поравняются друг с другом. Так как первый шел равномерно, а поезд (вместе с уезжающим) двигался равноускоренно, то запишем их уравнения движения в системе:
\[\left\{ \begin{gathered}
S = \frac{{{a_1}{t^2}}}{2} \hfill \\
S = {\upsilon _2}t \hfill \\
\end{gathered} \right.\]
Формула скорости в общем виде выглядит так:
\[\upsilon = {\upsilon _0} + at\]
Так как у поезда не было начальной скорости \(\upsilon _{01}=0\), то его скорость \(\upsilon_1\) определится так:
\[{\upsilon _1} = {a_1}t\]
Учитывая эту формулу, система примет вид:
\[\left\{ \begin{gathered}
S = \frac{{{\upsilon _1}t}}{2} \hfill \\
S = {\upsilon _2}t \hfill \\
\end{gathered} \right.\]
Поделим первое выражение системы на второе и выразим искомую скорость \(\upsilon_1\).
\[\frac{{{\upsilon _1}}}{{2{\upsilon _2}}} = 1 \Rightarrow {\upsilon _1} = 2{\upsilon _2}\]
\[{\upsilon _1} = 2 \cdot 3,5 = 7\; м/с = 25,2\; км/ч\]
Ответ: 25,2 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.20 Вертолет летит на высоте 500 м со скоростью 100 м/с. Навстречу ему по реке
1.7.22 Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется
1.7.23 Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после

 icodepro.ru
icodepro.ru