В последнюю секунду свободного падения тело прошло путь вдвое больше

Условие задачи:

В последнюю секунду свободного падения тело прошло путь вдвое больше, чем в предыдущую секунду. С какой высоты оно падало? (g=9,8 м/с²)

Задача №1.4.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_1=2S_2\), \(t_1=t_2=1\) с, \(g=9,8\) м/с², \(H-?\)

Решение задачи:

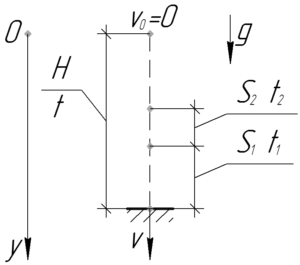Путь за последнюю секунду \(S_1\) – это разность пути за все время \(t\) и пути за \(\left( {t – {t_1}} \right)\) секунд. Аналогично, путь за предпоследнюю секунду \(S_2\) – это разность пути за \(\left( {t – {t_1}} \right)\) секунд и пути за \(\left( {t – {t_1}-{t_2}} \right)\) секунд. Аналитически это записывается так.

\[{S_1} = \frac{{g{t^2}}}{2} – \frac{{g{{\left( {t – {t_1}} \right)}^2}}}{2}\]

\[{S_2} = \frac{{g{{\left( {t – {t_1}} \right)}^2}}}{2} – \frac{{g{{\left( {t – {t_1} – {t_2}} \right)}^2}}}{2}\]

Так как по условию \(S_1=2S_2\), то справедливо:

\[{t^2} – {\left( {t – {t_1}} \right)^2} = 2{\left( {t – {t_1}} \right)^2} – 2{\left( {t – {t_1} – {t_2}} \right)^2}\]

Заменим \(t_1\) и \(t_2\) числами, тогда все сведется к следующему квадратному уравнению.

\[{t^2} – 3{\left( {t – 1} \right)^2} + 2{\left( {t – 2} \right)^2} = 0\]

Распишем два раза квадрат разности, в итоге получим:

\[{t^2} – 3{t^2} + 6t – 3 + 2{t^2} – 8t + 8 = 0\]

\[ – 2t + 5 = 0\]

\[t = 2,5\; с \]

Значит всего тело падало 2,5 с. Но это не ответ на вопрос задачи. Высоту, с которой бросили тело, можно найти по формуле:

\[H = \frac{{g{t^2}}}{2}\]

\[H = \frac{{9,8 \cdot {{2,5}^2}}}{2} = 30,6\; м \]

Ответ: 30,6 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.34 С вертолета, находящегося на высоте 300 м, сброшен груз. Через какое время
1.4.36 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м
1.4.37 Вертолет двигался равномерно вниз. Из вертолета выпал груз. Когда