Решение: В течение какого времени скорый поезд длиной 280 м, следуя со скоростью

Условие задачи:

В течение какого времени скорый поезд длиной 280 м, следуя со скоростью 72 км/ч, будет проходить мимо встречного товарного поезда длиной 700 м, идущего со скоростью 54 км/ч?

Задача №1.7.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L_1=280\) м, \(\upsilon_1=72\) км/ч, \(L_2=700\) м, \(\upsilon_2=54\) км/ч, \(t-?\)

Решение задачи:

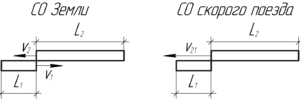Решать задачу начнем с того, что перейдем в систему отсчета (СО) первого (скорого) поезда. Понятно, что модуль скорости товарного поезда в СО скорого равен:

\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]

Это следует из правила сложения скоростей (обратное правило).

Когда мы находим в этой СО, то наш скорый поезд мысленно покоится, а товарный проходит мимо скорого с относительной скоростью. Время прохождения поездом мимо друг друга отсчитывается от момента встречи “голов” составов и заканчивается тогда, когда пройдут мимо друг друга их “хвосты”. Это станет сразу понятно, когда Вы посмотрите рисунок. Таким образом, будет пройдено суммарное расстояние, равное сумме длин двух поездов.

Тогда искомое время определяется из соотношения:

\[t = \frac{{{L_1} + {L_2}}}{{{\upsilon _{21}}}} = \frac{{{L_1} + {L_2}}}{{{\upsilon _1} + {\upsilon _2}}}\]

Чтобы получить верный ответ, переведем скорости, данные в условии, в систему СИ, то есть из км/ч в м/с.

\[72\; км/ч = \frac{{72 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{720}}{{36}\; м/с} = 20\; м/с\]

\[54\; км/ч = \frac{{54 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{540}}{{36}\; м/с} = 15\; м/с\]

Численный ответ равен:

\[t = \frac{{280 + 700}}{{20 + 15}} = 28\; с\]