Условие задачи:
Вертикально вверх с высоты 392 м с начальной скоростью 19,6 м/с брошено тело. Через какое время оно упадет на землю? (\(g=9,8\) м/с2)
Задача №1.4.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=392\) м, \(\upsilon_0=19,6\) м/с, \(g=9,8\) м/с2, \(t-?\)
Решение задачи:
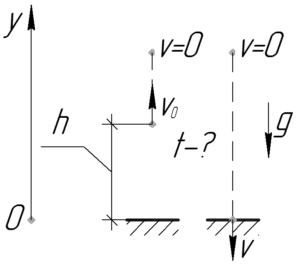 Приведем к задаче рисунок. Записывая уравнение движения тело вдоль оси \(y\), необходимо не забыть о том, что оно бросается не с земли (т.е. нулевой отметки оси), а с некоторой высоты \(h\).
Приведем к задаче рисунок. Записывая уравнение движения тело вдоль оси \(y\), необходимо не забыть о том, что оно бросается не с земли (т.е. нулевой отметки оси), а с некоторой высоты \(h\).
\[oy:y = h + {\upsilon _0}t — \frac{{g{t^2}}}{2}\]
Когда тело упадет на землю, его координата \(y\) будет равна нулю.
\[y = 0 \Rightarrow h + {\upsilon _0}t — \frac{{g{t^2}}}{2} = 0\]
В полученном квадратном уравнении одно неизвестное \(t\), т.е. решив уравнение, мы найдем ответ к задаче. Заменим буквенные обозначения величин численными, поскольку нет особого смысла получить ответ задачи в общем виде.
\[4,9{t^2} — 19,6t — 392 = 0\]
\[{t^2} — 4t — 80 = 0\]
Определим дискриминант \(D\).
\[D = 16 + 4 \cdot 80 = 336\]
\[t = \frac{{4 \pm \sqrt {336} }}{2} = 2 \pm \sqrt {84} \]
\[\left[ \begin{gathered}
t = 11,17 \; с \hfill \\
t = — 7,17 \; с \hfill \\
\end{gathered} \right.\]
Отрицательный корень не имеет смысла, поскольку отсчет времени начинается с нуля.
Ответ: 11,17 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.14 Мяч брошен вверх со скоростью 20 м/с. На какое расстояние от поверхности
1.4.16 Тело, свободно падающее из состояния покоя, в конце первой половины пути
1.4.17 Камень, брошенный вертикально вверх, упал на Землю через 2 с. Определить

 icodepro.ru
icodepro.ru
Почему в уравнение подставляют 392, если максимальная высота с которой падает тело 411,6?
Возможно ли решить данную задачу не прибегая к решению квадратного уравнения, а именно: 1)найти время от точки подъема до максимальной высоты через формулу v=v(0)-gt, это 2 сек. 2)найти высоту подъема тела от точки броска, это 19,6 м 3)найти общую высоту полета тела 392+19,6=411,6 4)найти время полета тела при падении через формулу s=gt^2/2? это 9,165 с 5)найти общее время полета 2+9,165=11,165 с
Возможно, но это решение не в общем виде.
А вообще, Ваше решение правильное (в том смысле, что Вы получили верный ответ).
Обычно просят предоставить общую формулу для решения задачи, чтобы в любой момент можно было поменять значения переменных задачи и вычислить просто подставив в формулы числа…