Условие задачи:
Вертолет летит на высоте 500 м со скоростью 100 м/с. Навстречу ему по реке движется катер со скоростью 20 м/с, на который с вертолета сбрасывают груз. На каком расстоянии от катера должен находиться вертолет в момент выброса груза?
Задача №1.7.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=500\) м, \(\upsilon_1=100\) м/с, \(\upsilon_2=20\) м/с, \(L-?\)
Решение задачи:
 Первое, о чем хотелось бы сказать — это то, что в момент выброса груза его скорость равна по величине и направлению скорости вертолета.
Первое, о чем хотелось бы сказать — это то, что в момент выброса груза его скорость равна по величине и направлению скорости вертолета.
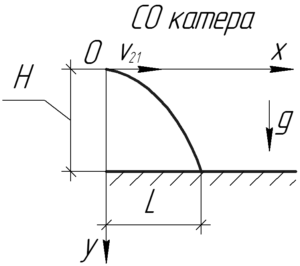
Поскольку в задаче мы имеем дело с относительным движением, то перейдем в систему отсчета (СО) катера. Чтобы определить вектор скорости груза \(\overrightarrow {{\upsilon _{21}}}\) в этой СО, необходимо к вектору его скорости относительно Земли \(\overrightarrow {{\upsilon _1}}\) прибавить вектор равный по величине и противоположный по направлению вектору скорости катера (\(— \overrightarrow {{\upsilon _2}}\)).
Поскольку груз и катер двигаются друг другу навстречу, то модуль вектора \(\overrightarrow {{\upsilon _{21}}}\) равен:
\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]
Запишем уравнения движения груза в проекциях на оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:x = {\upsilon _{21}}t \hfill \\
oy:y = \frac{{g{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Когда груз упадет на катер, то он пройдет по горизонтали расстояние \(L\), а по вертикали — высоту \(H\).
\[\left\{ \begin{gathered}
L = {\upsilon _{21}}t \;\;\;\;(1)\hfill \\
H = \frac{{g{t^2}}}{2} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Из выражения (2) найдем время падения:
\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}} \]
Подставим ранее полученные выражения в формулу (1), чтобы получить конечную формулу.
\[L = \left( {{\upsilon _1} + {\upsilon _2}} \right)\sqrt {\frac{{2H}}{g}} \]
Осталось только подсчитать ответ, подставив данные задачи.
\[L = \left( {100 + 20} \right)\sqrt {\frac{{2 \cdot 500}}{{10}}} = 1200\; м = 1,2\; км\]
Ответ: 1,2 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.19 Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду
1.7.21 В момент, когда тронулся поезд, провожающий стал равномерно бежать по ходу поезда
1.7.22 Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется

 icodepro.ru
icodepro.ru
Подождите. Вы ведь нашил расстояние от катера до самолета по OX, а нужно ведь все расстояние. Тоесть расстояние по OY и по OX. Это прямоугольный треугольник и по Т.Пифагора расстояние от самолета до катера = ?(5002+12002)=1300м. Не?