icodepro.ruУсловие задачи:
Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м из него выбрасывается вверх предмет со скоростью 2 м/с относительно вертолета. Через какое время предмет упадет на землю?
Задача №1.4.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=10\) м/с, \(\upsilon_0=2\) м/с, \(h=100\) м, \(t-?\)
Решение задачи:
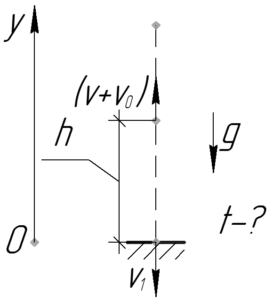Если тело кидают вверх со скоростью \(\upsilon_0\) относительно вертолета, а сам вертолет движется вверх со скоростью \(\upsilon\) относительно земли, то скорость тела в момент броска относительно земли равна \(\left( {{\upsilon _0} + \upsilon } \right)\).
Определившись с начальной скоростью, запишем уравнение движения предмета вдоль оси \(y\). Учтем, что тело имеет начальную координату, равную \(h\).
\[oy:y = h + \left( {{\upsilon _0} + \upsilon } \right)t – \frac{{g{t^2}}}{2}\]
Когда тело упадет на землю значение его координаты \(y\) будет равно нулю.
\[y = 0 \Rightarrow h + \left( {{\upsilon _0} + \upsilon } \right)t – \frac{{g{t^2}}}{2} = 0\]
Решим полученное уравнение, для этого подставим численные значения величин, встречающихся в нем.
\[100 + 12t – 5{t^2} = 0\]
\[5{t^2} – 12t – 100 = 0\]
\[D = 144 + 4 \cdot 5 \cdot 100 = 2144\]
\[t = \frac{{12 \pm \sqrt {2144} }}{{10}}\]
\[\left[ \begin{gathered}
t = 5,8 \; с \hfill \\
t = – 3,4 \; с \hfill \\
\end{gathered} \right.\]
Второй корень уравнения не может являться ответом к задаче, так как он отрицательный.
Ответ: 5,8 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.35 В последнюю секунду свободного падения тело прошло путь вдвое больше
1.4.37 Вертолет двигался равномерно вниз. Из вертолета выпал груз. Когда
1.4.38 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 50 м
