Условие задачи:

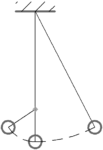Математический маятник с длиной нити $L$ совершает свободные колебания вблизи стены с частотой $\nu$. Чему будет равна частота колебаний такого маятника, если на одной вертикали с точкой подвеса в стену вбить гвоздь на расстоянии $\frac{3L}{4}$ от точки подвеса?

Задача №9.2.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$L$, $\nu$, $\frac{3L}{4}$, $\nu_1-?$

Решение задачи:

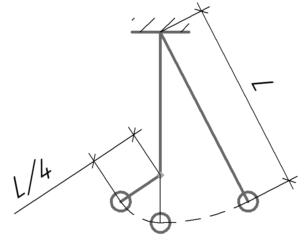Понятно, что мы будем иметь дело с двумя маятниками — один с длиной нити, равной $L$, а второй — с длиной нити, равной $\frac{L}{4}$. Запишем формулы для нахождения частот колебаний $\nu$ и $\nu’$ этих маятников:

$$\left\{ \begin{gathered} \nu = \frac{1}{{2\pi }}\sqrt {\frac{g}{L}} \hfill \\ \nu ‘ = \frac{1}{{2\pi }}\sqrt {\frac{{4g}}{L}} = \frac{1}{\pi }\sqrt {\frac{g}{L}} \hfill \\ \end{gathered} \right.$$

Откуда получим такое соотношение:

$$\nu ‘ = 2\nu \;\;\;\;(1)$$

Давайте разберемся с периодом колебаний получившегося маятника (после того, как в стену вобьют гвоздь). Достаточно легко понять, что этот период колебаний $T_1$ можно найти по формуле:

$${T_1} = \frac{T}{2} + \frac{{T’}}{2}$$

$${T_1} = \frac{{T + T’}}{2}$$

В этой формуле $T$ — период колебаний математического маятника с длиной нити $L$, а $T’$ — период колебаний математического маятника с длиной нити $\frac{L}{4}$.

Вполне понятно, что искомую частоту $\nu_1$ в таком случае можно найти по формуле:

$${\nu _1} = \frac{2}{{T + T’}}$$

Также, учитывая, что частота колебаний — это величина обратная периоду колебаний, имеем:

$${\nu _1} = \frac{2}{{\frac{1}{\nu } + \frac{1}{{\nu ‘}}}}$$

Учитывая (1), имеем:

$${\nu _1} = \frac{2}{{\frac{1}{\nu } + \frac{1}{{2\nu }}}}$$

$${\nu _1} = \frac{2}{{\frac{3}{{2\nu }}}}$$

$${\nu _1} = \frac{{4\nu }}{3}$$

Вот и всё, задача решена.

Ответ: $\frac{4{\nu}}{3}$.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.2.22 Небольшой металлический шарик массой 10 г, подвешенный на нити длиной 0,1 м
9.2.24 В неподвижном лифте период собственных колебаний математического маятника
9.3.1 Шарик массой 5 г колеблется по закону x=0,04*sin(2*pi*(t/T+0,5))