Решение: В струне, закрепленной с двух концов, возбуждены колебания. На рисунке показаны

Условие задачи:

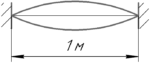В струне, закрепленной с двух концов, возбуждены колебания. На рисунке показаны положения струны в различные моменты времени. Длина струны 1 м, частота колебаний 340 Гц. Какова скорость распространения поперечных волн в струне?

Задача №9.6.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=1\) м, \(\nu=340\) Гц, \(\upsilon-?\)

Решение задачи:

Скорость распространения колебаний \(\upsilon\) можно определить через длину волны \(\lambda\) и частоту колебаний \(\nu\) следующим образом:

\[\upsilon = \lambda \nu \;\;\;\;(1)\]

На рисунке видно, что точки, в которых закреплена струна, колеблются с разностью фаз, равной \(\pi\). Если точки, находящиеся на расстоянии \(l\), колеблются с разностью фаз \(\pi\), а точки, находящиеся на расстоянии \(\lambda\) — c разностью фаз \(2\pi\), то справедливо записать следующее соотношение:

\[\frac{l}{\pi } = \frac{\lambda }{{2\pi }}\]

Выразим отсюда длину волны \(\lambda\):

\[\lambda = 2l\;\;\;\;(2)\]

Подставим выражение (2) в формулу (1), тогда получим:

\[\upsilon = 2\nu l\]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[\upsilon = 2 \cdot 340 \cdot 1 = 680\;м/с\]