icodepro.ruУсловие задачи:
Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона к горизонту 45°, имея скорость 6 м/с у основания. На какую высоту она поднимется, если коэффициент трения равен 0,2?
Задача №2.3.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=45^\circ\), \(\upsilon_0=6\) м/с, \(\mu=0,2\), \(H-?\)
Решение задачи:
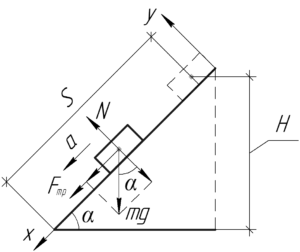На схеме покажем все силы, действующие на льдинку. Введем оси координат так, что ось \(y\) направим перпендикулярно наклонной плоскости, а ось \(x\) — вдоль плоскости. Понятно, что льдинка будет двигаться равнозамедленно, так как проекция силы тяжести на ось \(x\) и сила трения скольжения будут её тормозить. Запишем второй закон Ньютона в проекции на ось \(x\):
\[ma = mg \cdot \sin \alpha + {F_{тр}}\;\;\;\;(1)\]
Так как льдинка не движется вдоль оси \(y\), то запишем первый закон Ньютона в проекции на эту ось:
\[N = mg \cdot \cos \alpha \;\;\;\;(2)\]
Силу трения скольжения определим по известной формуле:
\[{F_{тр}} = \mu N\]
Учитывая (2), формула определения силы трения примет вид:
\[{F_1} = \mu mg \cdot \cos \alpha \]
Подставим полученное в (1), определим ускорение \(a\):
\[ma = mg \cdot \sin \alpha + \mu mg \cdot \cos \alpha \]
\[a = g\left( {\sin \alpha + \mu \cos \alpha } \right)\;\;\;\;(3)\]
В конце концов льдинка остановится, пройдя путь вдоль оси \(x\), равный \(S\). Применим следующую формулу из кинематики:
\[0 — \upsilon _0^2 = — 2aS\]
Выразим путь \(S\):
\[S = \frac{{\upsilon _0^2}}{{2a}}\;\;\;\;(4)\]
Если посмотреть на схему, то понятно, что льдинка поднимется на высоту \(H\), определяемую соотношением:
\[H = S \cdot \sin \alpha \]
Подставим (3) в (4), а полученное — в последнюю формулу, тогда:
\[H = \frac{{\upsilon _0^2 \cdot \sin \alpha }}{{2g\left( {\sin \alpha + \mu \cos \alpha } \right)}}\]
Поделим числитель и знаменатель на \(\sin \alpha\), так мы получим решение задачи в общем виде:
\[H = \frac{{\upsilon _0^2}}{{2g\left( {1 + \mu \cdot ctg\alpha } \right)}}\]
Посчитаем численный ответ:
\[H = \frac{{{6^2}}}{{2 \cdot 10 \cdot \left( {1 + 0,2 \cdot ctg45^\circ } \right)}} = 1,5\; м\]
Ответ: 1,5 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.1 Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
между 3 и 4 формулой есть формула. Почему в ней написано МИНУС 2aS?
S= Uво второй минус U0 во второй поделенное на 2а… А значит 0-U0 во второй равно просто 2аS… Разве нет?
Или это из-за того что тело замедляется?
Да, именно из-за того, что тело замедляется. Вы должны из квадрата конечной скорости вычесть квадрат начальной скорости. Если тело замедляется, то есть \({\upsilon _0} < \upsilon \), то \({\upsilon ^2} - \upsilon _0^2 < 0\), поэтому в правой части должен быть знак "минус".
Подскажите, пожалуйста, почему в формуле 0 – (v_0)^2 = – 2*a*S, правая часть уравнения с минусом, ведь ускорение согласно схеме направлено в туже сторону, что и ось Х, т.е. положительно?
Сейчас все объясню. Эта формула в векторном виде записывается так:\[{\overrightarrow \upsilon ^2} — {\overrightarrow {{\upsilon _0}} ^2} = 2\overrightarrow a \cdot \overrightarrow S \]Здесь мы видим аж три скалярных произведения векторов. Скалярное произведение векторов в правой части этой формулы раскрывается следующим образом:\[\overrightarrow a \cdot \overrightarrow S = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow S } \right| \cdot \cos \left( {\overrightarrow a \wedge \overrightarrow S } \right)\]Если у Вас вектор ускорения сонаправлен с вектором перемещения, то косинус будет положительным, иначе — отрицательным. Вот так определяется знак в правой части этой формулы.
Это объяснение наиболее полное. Есть проще: смотрите какой у Вас будет знак в левой части, такой же знак ставьте и в правой.
как вы получили тангенс?
Там должен быть котангенс, в решении была ошибка, а ответ получался правильный только из-за того, что угол \(\alpha\) равен 45°.
Спасибо за замечание, решение откорректировано!
А по формуле t=v°:a и h=v°xt- at2:2 решить тоже можно или я не прав?
Конечно можете, но в вашем случае h — это расстояние, пройденное льдинкой вдоль наклонной плоскости, а это не совсем то, что мы ищем в этой задаче.
Чтобы найти H, Вам также будет необходимо применить формулу:
H= h*sin a
Вообще, любопытства ради, подставьте t=v_0/a в h=v_0*t — at2/2. Вы получите:
0 — (v_0)^2 = — 2*a*S
Этим я хочу сказать, что Вы просто лишний раз удлиняете решение. Зачем Вам возиться с временем, если о нем не спрашивают и в условии о нём не говорится?