Решение: Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление

Условие задачи:

Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление на снег станет равным нулю, если траекторию на данном участке можно считать дугой окружности радиусом \(R=80\) м. Трением пренебречь.

Задача №2.4.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=80\) м, \(h-?\)

Решение задачи:

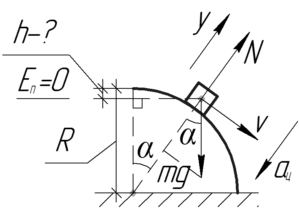Запишем второй закон Ньютона в проекции на ось \(y\) для того момента, когда лыжник перестанет давить на снег.

\[ — mg \cdot \cos \alpha + N = — m{a_ц}\;\;\;\;(1)\]

Если давление лыжника на снег станет равным нулю, значит в этой точке сила реакции опоры \(N\) равна нулю по третьему закону Ньютона, то есть лыжник оторвется от снега.

\[N = 0\;\;\;\;(2)\]

Пусть скорость лыжника в этой точке отрыва равна \(\upsilon\). Учитывая, что траектория его движения имеет радиус кривизны \(R\), то центростремительное ускорение \(a_ц\) найдем по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]

С учетом выражений (2) и (3), равенство (1) примет такой вид:

\[mg \cdot \cos \alpha = m\frac{{{\upsilon ^2}}}{R}\]

\[{\upsilon ^2} = gR \cdot \cos \alpha \;\;\;\;(4)\]

Кстати, из схемы очень просто найти косинус угла \(\alpha\), он равен:

\[\cos \alpha = \frac{{R — h}}{R}\]

Равенство (4) уже станет таким:

\[{\upsilon ^2} = g\left( {R — h} \right)\;\;\;\;(5)\]

Теперь применим закон сохранения энергии, так как неконсервативные силы (сила трения, сила сопротивления воздуха) отсутствуют. Для этого выберем нуль отсчета потенциальной энергии на уровне точки отрыва лыжника от снега.

\[mgh = \frac{{m{\upsilon ^2}}}{2}\]

\[{\upsilon ^2} = 2gh\;\;\;\;(6)\]

Приравняем правые стороны (5) и (6):

\[g\left( {R — h} \right) = 2gh\]

\[R — h = 2h\]

\[h = \frac{R}{3}\]

Считаем ответ:

\[h = \frac{{80}}{3} = 26,7\; м\]