icodepro.ruУсловие задачи:
Электрон с энергией 4,2·10-18 Дж влетает в однородное магнитное поле с индукцией 0,3 Тл перпендикулярно силовым линиям. Определить радиус траектории электрона.
Задача №8.2.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(W=4,2 \cdot 10^{-18}\) Дж, \(B=0,3\) Тл, \(\alpha=90^\circ\), \(R-?\)
Решение задачи:
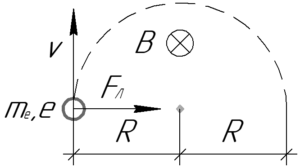На электрон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(1)\]
Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость электрона, \(e\) — модуль заряда электрона, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.
Сила Лоренца \(F_Л\) сообщает электрону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:
\[{F_Л} = {m_e}{a_ц}\;\;\;\;(2)\]
Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]
Подставим (3) в (2), тогда:
\[{F_Л} = \frac{{{m_e}{\upsilon ^2}}}{R}\;\;\;\;(4)\]
Приравняем правые части (1) и (4):
\[B\upsilon e\sin \alpha = \frac{{{m_e}{\upsilon ^2}}}{R}\]
Имеем:
\[Be\sin \alpha = \frac{{{m_e}\upsilon }}{R}\]
\[R = \frac{{{m_e}\upsilon }}{{Be\sin \alpha }}\;\;\;\;(5)\]
Кинетическая энергия электрона \(W\) равна:
\[W = \frac{{{m_e}{\upsilon ^2}}}{2}\]
Выразим из этой формулы неизвестную скорость электрона \(\upsilon\):
\[\upsilon = \sqrt {\frac{{2W}}{{{m_e}}}} \;\;\;\;(6)\]
Осталось только подставить выражение (6) в формулу (5):
\[R = \frac{{{m_e}}}{{Be\sin \alpha }}\sqrt {\frac{{2W}}{{{m_e}}}} \]
\[R = \frac{{\sqrt {2W{m_e}} }}{{Be\sin \alpha }}\]
Напомним, что масса электрона \(m_e\) равна 9,1·10-31 кг, а его заряд \(e\) (вернее модуль заряда) равен 1,6·10-19 Кл. Численный ответ равен:
\[R = \frac{{\sqrt {2 \cdot 4,2 \cdot {{10}^{ — 18}} \cdot 9,1 \cdot {{10}^{ — 31}}} }}{{0,3 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot \sin 90^\circ }} = 5,76 \cdot {10^{ — 5}}\;м = 57,6\;мкм\]
Ответ: 57,6 мкм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.1.21 Провод длиной 20 см с током 10 А перемещается в однородном магнитном поле с индукцией
8.2.2 На частицу со стороны однородного магнитного поля действует сила Лоренца, равная
8.2.3 Электрон и протон, двигаясь с одинаковыми скоростями, влетают в однородное магнитное
Для начала, нам нужно использовать формулу для радиуса траектории заряженной частицы в магнитном поле:
r = (mv)/(qB)
где r — радиус траектории, m — масса электрона, v — скорость электрона, q — заряд электрона и B — индукция магнитного поля.
Мы знаем, что электрон имеет энергию 4,210-18 Дж, что можно использовать для определения скорости электрона. Мы также знаем, что индукция магнитного поля равна 0,3 Тл. Значение заряда электрона известно и составляет -1,602 x 10^-19 Кл.
Таким образом, мы можем решить задачу, подставив известные значения в формулу:
r = (mv)/(qB)
r = ((2 * 4,210-18) / (9,109 * 10^-31)) / ((-1,602 * 10^-19) * 0,3)
r = 0,000003 метра
Таким образом, радиус траектории электрона составляет 0,000003 метра.
Для решения задачи необходимо использовать формулу для радиуса Лармора: r = (mv?)/qB, где m — масса электрона, v? — скорость электрона, перпендикулярная магнитному полю, q — заряд электрона, B — индукция магнитного поля.
Масса электрона m = 9,11·10^-31 кг, заряд q = -1,6·10^-19 Кл (знак — потому что электрон отрицательно заряжен).
Скорость электрона можно найти из формулы для кинетической энергии: Eк = mv^2/2, v = ?(2Eк/m).
Подставляя заданные значения, получаем: v = ?(2·4,2·10^-18/9,11·10^-31) ? 1,956·10^6 м/c.
Подставляем найденные значения в формулу для радиуса Лармора: r = (m·v?)/(q·B) = (m·v)/(q·B).
Подставляем найденные значения: r = (9,11·10^-31·1,956·10^6)/(1,6·10^-19·0,3) ? 0,20 мм.
Добрый день, а почему четыре вытянутых пальца нужно направить против направления отрицательного заряда?
Потому что в правиле левой руке Вы должны расположить четыре вытянутых пальца по направлению положительного заряда, а у нас в задаче речь идет об электроне, который имеет отрицательный заряд. В случае отрицательного заряда четыре вытянутых пальца располагаете против направления движения отрицательного заряда.
Благодарю