Условие задачи:
Из проволоки длиной 20 см сделали квадратный контур. Найти максимальный вращающий момент сил, действующий на контур, помещенный в магнитное поле с индукцией 0,1 Тл. По контуру течет ток 2 А.
Задача №8.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(L=20\) см, \(B=0,1\) Тл, \(I=2\) А, \(M_{\max}-?\)
Решение задачи:
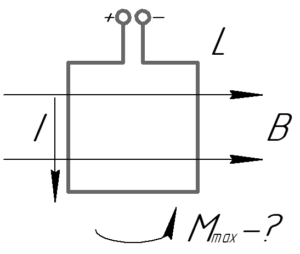 Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил \(M\), который можно найти по следующей формуле:
Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил \(M\), который можно найти по следующей формуле:
\[M = BIS\sin \alpha \]
В этой формуле \(B\) — индукция магнитного поля, \(I\) — сила текущего в рамке (контуре) тока, \(S\) — площадь рамки (контура), \(\alpha\) — угол между нормалью к плоскости контура и вектором магнитной индукции.
Очевидно, что максимальный магнитный момент будет наблюдаться тогда, когда угол \(\alpha\) между нормалью к плоскости контура и вектором магнитной индукции будет равен 90°, то есть плоскость контура будет параллельна линиям магнитной индукции (смотрите рисунок к задаче). Поэтому:
\[{M_{\max }} = BIS\;\;\;\;(1)\]
Понятно, что если из проволоки длиной \(L\) сделать квадратный контур, то длина стороны этого контура \(a\) будет равна:
\[a = \frac{L}{4}\]
В таком случае, площадь квадратного контура \(S\) будет равна:
\[S = {a^2}\]
\[S = \frac{{{L^2}}}{{16}}\]
Учитывая это, формула (1) примет вид:
\[{M_{\max }} = \frac{{BI{L^2}}}{{16}}\]
Посчитаем теперь численный ответ к задаче:
\[{M_{\max }} = \frac{{0,1 \cdot 2 \cdot {{0,2}^2}}}{{16}} = 5 \cdot {10^{ — 4}}\;Н \cdot м\]
Ответ: 5·10-4 Н·м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.3.14 Определить индукцию однородного магнитного поля, если на прямоугольную рамку
8.3.16 Определить вращающий момент плоского контура площадью 0,04 м2, помещенного
8.3.17 Определить поток вектора магнитной индукции через плоскую поверхность площадью

 icodepro.ru
icodepro.ru