Условие задачи:

Магнитная индукция однородного магнитного поля равна 4 Тл. Какой магнитный поток пройдет через площадку в 50 см², расположенную перпендикулярно вектору магнитной индукции?

Задача №8.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(B=4\) Тл, \(S=50\) см², \(\beta=90^\circ\), \(\Phi-?\)

Решение задачи:

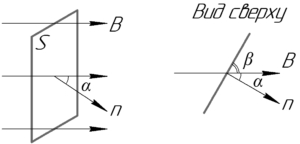Магнитный поток через некоторую площадку, помещённую в однородном магнитном поле, можно определить по такой формуле:

\[\Phi = BS\cos \alpha \;\;\;\;(1)\]

В этой формуле \(B\) — индукция магнитного поля, \(S\) — площадь поверхности, через которую определяется магнитный поток, \(\alpha\) — угол между нормалью к площадке и вектором магнитной индукции.

Обратите свое внимание на то, что в условии дан угол \(\beta\) между площадкой и вектором магнитной индукции (или направлением, что то же самое), а не угол \(\alpha\) между нормалью к площадке и вектором магнитной индукции. Тем не менее на рисунке видно, что эти углы связаны между собой по формуле:

\[\alpha = 90^\circ — \beta \]

С учётом этого, формула (1) примет вид:

\[\Phi = BS\cos \left( {90^\circ — \beta } \right)\]

\[\Phi = BS\sin \beta \]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[\Phi = 4 \cdot 50 \cdot {10^{ — 4}} \cdot \sin 90^\circ = 0,02\;Вб\]

Ответ: 0,02 Вб.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.3.7 Определить изменение магнитного потока через катушку, если она имеет 2000 витков
8.3.9 Рамка площадью 100 см2 расположена перпендикулярно линиям магнитной индукции
8.3.10 Магнитная индукция однородного магнитного поля равна 0,5 Тл. Найти магнитный поток

Страсть, ласку и свое красивое тело, проверенные феи проститутки Екатеринбург с feiekb.com готовы на многое, ради вашего удовольствия. Вы можете воспользоваться услугами проститутки тогда, когда этого пожелаете, достаточно сделать один звонок и договориться о встрече. Позитивные проверенные феи проститутки Екатеринбург, горячие и прелестные, они такие интересные и чуткие, что удовольствие неизбежно. Выбери девушку сейчас.