Решение: Определить вращающий момент плоского контура площадью 0,04 м2, помещенного

Условие задачи:

Определить вращающий момент плоского контура площадью 0,04 м², помещенного в однородное магнитное поле с индукцией 20 Тл, если по контуру течет ток 10 А, а плоскость контура составляет с линиями индукции угол 30°.

Задача №8.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S=0,04\) м², \(B=20\) Тл, \(I=10\) А, \(\beta=30^\circ\), \(M-?\)

Решение задачи:

Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил \(M\), который можно найти по следующей формуле:

\[M = BIS\sin \alpha \;\;\;\;(1)\]

В этой формуле \(B\) — индукция магнитного поля, \(I\) — сила текущего в рамке (контуре) тока, \(S\) — площадь рамки (контура), \(\alpha\) — угол между нормалью к плоскости рамки (контура) и вектором магнитной индукции.

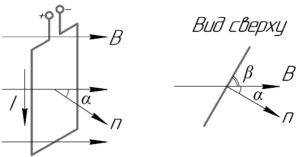
Обратите свое внимание на то, что в условии дан угол \(\beta\) между плоскостью контура и вектором магнитной индукции (или направлением, что то же самое), а не угол \(\alpha\) между нормалью к площадке и вектором магнитной индукции. Тем не менее на рисунке видно, что эти углы связаны между собой по формуле:

\[\alpha = 90^\circ — \beta \]

Учитывая это, формула (1) примет вид:

\[M = BIS\sin \left( {90^\circ — \beta } \right)\]

Так как из тригонометрии известно, что \(\sin \left( {90^\circ — \beta } \right) = \cos \beta\), то:

\[M = BIS\cos \beta \]

Задача решена в общем виде, теперь посчитаем численный ответ:

\[M = 20 \cdot 10 \cdot 0,04 \cdot \cos 30^\circ = 6,93\;Н \cdot м\]