Решение: Рамка площадью 100 см2 расположена перпендикулярно линиям магнитной индукции

Условие задачи:

Рамка площадью 100 см² расположена перпендикулярно линиям магнитной индукции (\(B=0,2\) Тл). На сколько изменится поток магнитной индукции через рамку, если её повернуть на 180°?

Задача №8.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S=100\) см², \(\beta=90^\circ\), \(B=0,2\) Тл, \(\gamma=180^\circ\), \(\Delta \Phi-?\)

Решение задачи:

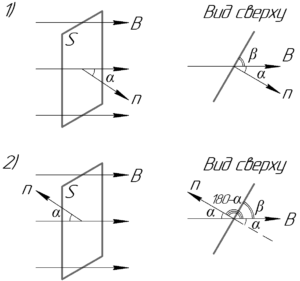Магнитный поток через площадку рамки, помещённой в однородном магнитном поле, можно определить по такой формуле:

\[\Phi = BS\cos \alpha\]

В этой формуле \(B\) — индукция магнитного поля, \(S\) — площадь поверхности рамки, через которую определяется магнитный поток, \(\alpha\) — угол между нормалью к рамке и вектором магнитной индукции.

Понятно, что если рамку повернуть на угол \(\gamma\), равный 180°, то угол между нормалью к рамке и вектором магнитной индукции станет равным \(\left( {180^\circ — \alpha } \right)\), поскольку вместе с рамкой повернется и вектор нормали к рамке (смотрите рисунок к задаче).

Учитывая вышесказанное, начальный и конечный поток магнитной индукции равен:

\[\left\{ \begin{gathered}
{\Phi _1} = BS\cos \alpha \hfill \\
{\Phi _2} = BS\cos \left( {180^\circ — \alpha } \right) \hfill \\
\end{gathered} \right.\]

Так как \(\cos \left( {180^\circ — \alpha } \right) = — \cos \alpha\), то:

\[\left\{ \begin{gathered}
{\Phi _1} = BS\cos \alpha \hfill \\
{\Phi _2} = — BS\cos \alpha \hfill \\
\end{gathered} \right.\]

Искомое изменение потока магнитной индукции равно:

\[\Delta \Phi = {\Phi _1} — {\Phi _2}\]

\[\Delta \Phi = BS\cos \alpha — \left( { — BS\cos \alpha } \right)\]

\[\Delta \Phi = 2BS\cos \alpha \;\;\;\;(1)\]

Обратите свое внимание на то, что в условии дан угол \(\beta\) между площадкой и вектором магнитной индукции (или направлением, что то же самое), а не угол \(\alpha\) между нормалью к площадке и вектором магнитной индукции. Тем не менее на рисунке видно, что эти углы связаны между собой по формуле:

\[\alpha = 90^\circ — \beta \]

С учётом этого, формула (1) примет вид:

\[\Delta \Phi = 2BS\cos \left( {90^\circ — \beta } \right)\]

\[\Delta \Phi = 2BS\sin \beta \]

Задача решена, теперь посчитаем ответ:

\[\Delta \Phi = 2 \cdot 0,2 \cdot 100 \cdot {10^{ — 4}} \cdot \sin 90^\circ = 0,004\;Вб = 4\;мВб\]