Условие задачи:
В магнитном поле с индукцией 0,01 Тл вращается стержень длиной 0,2 м с постоянной угловой скоростью 100 рад/с. Определить ЭДС индукции, возникающую в стержне, если ось вращения проходит через конец стержня параллельно линиям индукции магнитного поля.
Задача №8.4.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(B=0,01\) Тл, \(l=0,2\) м, \(\omega=100\) рад/с, \(\rm E_i-?\)
Решение задачи:
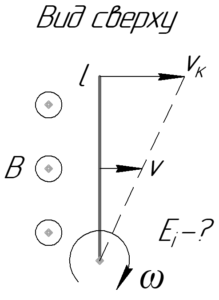 В данном случае ЭДС индукции в стержне \(\rm E_i\), вращающемся в магнитном поле, нужно определять по такой формуле:
В данном случае ЭДС индукции в стержне \(\rm E_i\), вращающемся в магнитном поле, нужно определять по такой формуле:
\[{{\rm E}_i} = B\upsilon l\;\;\;\;(1)\]
В этой формуле \(B\) — индукция магнитного поля, \(\upsilon\) — скорость центра масс стержня (т.е. скорость середины проводника), \(l\) — длина стержня.
На рисунке показано распределение скоростей точек стержня, например, \(\upsilon_к\) — это скорость конца стержня. Очевидно, что точка стержня, находящаяся на оси вращения, имеет нулевую скорость. В этой задаче важно понять, что в формуле (1) используется именно скорость середины стержня \(\upsilon\).
Скорость центра масс стержня \(\upsilon\) легко найти по формуле:
\[\upsilon = \frac{{\omega l}}{2}\;\;\;\;(2)\]
Подставим выражение (2) в формулу (1):
\[{{\rm E}_i} = \frac{{B\omega {l^2}}}{2}\]
Подставим данные задачи в эту формулу и посчитаем численный ответ:
\[{{\rm E}_i} = \frac{{0,01 \cdot 100 \cdot {{0,2}^2}}}{2} = 0,02\;В\]
Ответ: 0,02 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.49 Поток магнитной индукции в проводящем контуре, содержащем 100 витков
8.4.51 Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся
8.4.52 При равномерном изменении силы тока через катушку из 500 витков в ней возникает

 icodepro.ru
icodepro.ru