Условие задачи:
Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону \(\upsilon=10-2t\) (м/с). На сколько изменится импульс материальной точки за 4 с.
Задача №2.1.62 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=1\) кг, \(\upsilon=10-2t\) м/с, \(\Delta t=4\) с, \(\Delta p-?\)
Решение задачи:
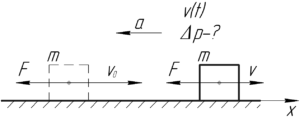 Запишем второй закон Ньютона в двух формах его записи:
Запишем второй закон Ньютона в двух формах его записи:
\[\left\{ \begin{gathered}
F = ma \hfill \\
F = \frac{{\Delta p}}{{\Delta t}} \hfill \\
\end{gathered} \right.\]
Приравняв оба выражения, получим:
\[ma = \frac{{\Delta p}}{{\Delta t}}\]
\[\Delta p = ma \cdot \Delta t\]
Формула изменения скорости при прямолинейном равнозамедленном движении выглядит так:
\[\upsilon = {\upsilon _0} — at\]
Сравнивая с законом изменения скорости, данным в условии, можно прийти в следующим выводам:
\[\left\{ \begin{gathered}
{\upsilon _0} = 10\; м/с \hfill \\
a = 2\; м/с^2 \hfill \\
\end{gathered} \right.\]
В итоге изменение импульса составит:
\[\Delta p = 1 \cdot 2 \cdot 4 = 8\; кг \cdot м/с\]
Так как закон изменения скорости убывающий, то импульс уменьшится на 8 кг·м/с.
Ответ: уменьшится на 8 кг·м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.61 Дождевая капля массой 0,02 г под влиянием горизонтально дующего ветра падает
2.1.63 Канат лежит на плоской горизонтальной крыше так, что часть его свешивается
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с

 icodepro.ru
icodepro.ru
проще графически представит процесс изменения импульса от времени
а почему пропал минус у ускорения
Я находил абсолютную величину изменения импульса (т.е. модуль), а характер этого изменения (уменьшился ли импульс или увеличился) уже определил исходя из закона изменения скорости
В задаче не говорится, что надо найти модуль изменения импульса.
Знак пропал. Решение не верно.
Эдак, мы в каждой задаче будем искать то, что не прописано.
Можно ли в данной задаче воспользоваться законом сохранения импульса: отнять от импульса с начальной скоростью при нулевом времени импульс со второй скоростью (подставляя изменение времени в формулу скорости)? Т.е. mv(0)-mv(2)?
Да, можно, но ни о каком законе сохранения импульса речи не идет. Сами посудите: импульс же меняется, так как на тело действует сила.