Решение: Даны две изохоры для одной и той же массы идеального газа

Условие задачи:

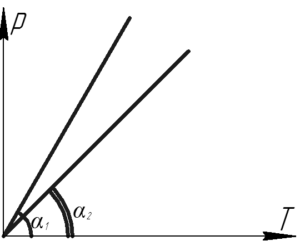Даны две изохоры для одной и той же массы идеального газа. Чему равно соотношение плотностей газа в первом и втором случаях, если \(\alpha_1=60^\circ\), \(\alpha_2=45^\circ\)? Рисунок, данный в условии к задаче, приведен справа.

Задача №4.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha_1=60^\circ\), \(\alpha_2=45^\circ\), \(\frac{{{\rho _1}}}{{{\rho _2}}} – ?\)

Решение задачи:

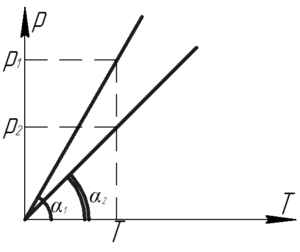Рисунок, поясняющий решение, приведем справа.

Начнем издалека, сначала запишем уравнение Клапейрона-Менделеева:

\[pV = \frac{m}{M}RT\]

Так как нам необходимо найти соотношение плотностей, то выразим ее из уравнения. Общеизвестно, что плотность – это соотношение массы газа к его объему:

\[\rho = \frac{m}{V}\]

Тогда:

\[p = \frac{\rho }{M}RT \Rightarrow \rho = \frac{{pM}}{{RT}}\]

Запишем последнее выражение в виде:

\[\rho = \frac{p}{T} \cdot \frac{M}{R}\]

Дробь \(\frac{M}{R}\) остается постоянной, поскольку в газовых процессах молярная масса газа и газовая постоянная никогда не меняются (по крайней мере я иного не встречал).

Теперь, если взглянуть на рисунок к решению задачи, то можно увидеть, что соотношение \(\frac{p}{T}\) для первого и второго процесса можно выразить тригонометрической функцией заданных углов. Для первого процесса – это тангенс угла \(\alpha_1\), а для второго – \(\alpha_2\).

Тогда отношение плотностей газа в двух процессах – это отношение тангенсов углов наклона графика:

\[\frac{{{\rho _1}}}{{{\rho _2}}} = \frac{{tg{\alpha _1}}}{{tg{\alpha _2}}}\]

\[\frac{{{\rho _1}}}{{{\rho _2}}} = \frac{{tg60^\circ }}{{tg45^\circ }} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \approx 1,73\]