Условие задачи:
Давление азота в электрической лампочке объемом 0,15 л равно 68 кПа. Сколько воды войдет в лампочку, если у нее отломить кончик под поверхностью воды? Атмосферное давление нормальное.
Задача №4.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_0=0,15\) л, \(p_0=68\) кПа, \(m-?\)
Решение задачи:
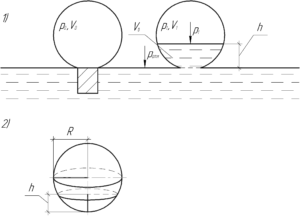 Скажу честно, что с точки зрения физики задача простая. Кончик лампочки погрузили в воды, далее этот кончик отламывают, а поскольку давление в лампочке меньше атмосферного, то в ее полость устремляется вода. Будем считать, что процесс настолько быстрый, что температура не успеет поменяться, то есть он изотермический (\(T=const\)). Запишем закон Бойля-Мариотта, предварительно изобразив процесс на рисунке (схема под номером 1).
Скажу честно, что с точки зрения физики задача простая. Кончик лампочки погрузили в воды, далее этот кончик отламывают, а поскольку давление в лампочке меньше атмосферного, то в ее полость устремляется вода. Будем считать, что процесс настолько быстрый, что температура не успеет поменяться, то есть он изотермический (\(T=const\)). Запишем закон Бойля-Мариотта, предварительно изобразив процесс на рисунке (схема под номером 1).
\[{p_0}{V_0} = {p_1}{V_1}\;\;\;\; (1)\]
Давление на поверхности жидкости равно атмосферному и оно уравновешивается конечным давлением газа в лампочке и столбом воды высотой \(h\) (см. рисунок, схема 1), поэтому:
\[{p_{атм}} = {p_1} + \rho gh\;\;\;\; (2)\]
Конечный объем, занимаемый азотом, равен разности объема лампочки и объема, занимаемого водой в конце процесса.
\[{V_1} = {V_0} — {V_в}\;\;\;\; (3)\]
Выразив \(p_1\) из формулы (2), подставим полученное и формулу (3) в формулу (1), тогда получим:
\[{p_0}{V_0} = \left( {{p_{атм}} — \rho gh} \right)\left( {{V_0} — {V_в}} \right)\;\;\;\; (4)\]
Необходимо знать, как сосчитать объем воды, проникшей в лампочку. Эта задача сводиться к вычислению объема шарового сегмента (смотри схему 2 на рисунке). Оказывается, она зависит от высоты шарового сегмента \(h\) и радиуса шара \(R\) и определяется по формуле:
\[{V_в} = \pi {h^2}\left( {R — \frac{h}{3}} \right)\]
Но нам не известен радиус шара, выразим его из известного объема шарообразной лампочки:
\[{V_0} = \frac{4}{3}\pi {R^3}\]
\[R = \sqrt[3]{{\frac{{3{V_0}}}{{4\pi }}}}\;\;\;\; (5)\]
В итоге формула (4) примет вид:
\[{p_0}{V_0} = \left( {{p_{атм}} — \rho gh} \right)\left( {{V_0} — \pi {h^2}\left( {R — \frac{h}{3}} \right)} \right)\]
В этом уравнении одно неизвестное \(h\) (радиус шара \(R\) можно найти численно). Решить задачу в общем виде не представляется возможным, поэтому подставим в это уравнение исходные данные в системе СИ. Тогда решив это уравнение 4-той степени мы получим численные значения \(h\) также в системе СИ, т.е. в метрах.
Вычислим для начала численно радиус лампочки по формуле (5):
\[R = \sqrt[3]{{\frac{{3 \cdot 15 \cdot {{10}^{ — 5}}}}{{4 \cdot 3,14}}}} = 0,033\; м\]
\[68 \cdot {10^3} \cdot 15 \cdot {10^{ — 5}} = \left( {{{10}^5} — {{10}^3} \cdot 10 \cdot h} \right)\left( {15 \cdot {{10}^{ — 5}} — 3,14 \cdot {h^2}\left( {0,033 — \frac{h}{3}} \right)} \right)\]
\[10,2 = \left( {{{10}^5} — {{10}^4}h} \right)\left( {0,00015 — 0,1037{h^2} + 1,0472{h^3}} \right)\]
После раскрытия скобок и приведения всех подобных слагаемых получается следующее уравнение четвертой степени:
\[10472{h^4} — 105757{h^3} + 10370{h^2} + 1,5h — 4,8 = 0\]
Уравнение отлично решается c помощью сайта Wolfram Alpha и имеет следующие корни:
\[\left[ \begin{gathered}
h = — 0,0196904\; м \hfill \\
h = 0,0247813\; м \hfill \\
h = 0,0939361\; м \hfill \\
h = 10\; м \hfill \\
\end{gathered} \right.\]
Все корни, кроме второго не подходят как решения, поскольку первый корень — отрицателен, а третий и четвертый — больше чем два радиуса (уровень воды не может быть больше диаметра лампочки).
Массу воды, вошедшую в лампочку, найдем через ее объем (по формуле шарового сегмента, смотри выше) и плотность:
\[m = \rho {V_{в}}\]
\[m = \rho \pi {h^2}\left( {R — \frac{h}{3}} \right)\]
В итоге:
\[m = {10^3} \cdot 3,14 \cdot {0,0247813^2}\left( {0,033 — \frac{{0,0247813}}{3}} \right) = 0,0477\; кг\]
Честно говоря, я не знаю более простого решения. С точки зрения математики задача очень сложная, но легко решается при наличии доступа к компьютеру.
Ответ: 0,048 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.3.23 Газ занимает объем 8 л при температуре 300 К. Определите массу газа
4.3.25 Бутылка с газом закрыта пробкой, площадь сечения которой 2,5 см2
4.3.26 В цилиндре под поршнем находится газ. Масса поршня 0,6 кг

 icodepro.ru
icodepro.ru
Мне нравится, что 23-я задача на простенькую формулу, а в 24-ой нужно решать уравнение 4-ой степени
У уууу реклама
Можно ли решать найдя объем азота при нормальном давлении, и если вычесть его из всего объема найдем объем воды
Вы считаете, что после того, как у лампочки отломят кончик, давление азота внутри лампочки будет атмосферным. Но я не могу понять почему. Если это предположение верно, то да, так можно решать.
Скорее всего там давление немного больше атмосферного, но при решении считают, что оно равно атмосферному. В таком случае Ваш ход мыслей верен. Ваше решение будет гораздо короче.
Можно пренебречь давлением, которое оказывает вода. Допустим что вода полностью заполнит лампочку радиусом 0.033м. Тогда Давление воды pgl=1000*10*0.033=330 Па. Это много меньше, чем давление газа, а учитывая, что вода заполнит не всю лампочку, то давление и подавно будет меньше. Тогда Просто считаем, что газ внутри лампочки под нормальным давлением, а дальше просто по закону Бойля-Мариотта.
Все верно! Скоро поправлю решение
щиВЧ