Условие задачи:

Давление воздуха в сосуде 97 кПа. После трёх ходов откачивающего поршневого насоса давление упало до 28,7 кПа. Определить отношение объемов сосуда и цилиндра насоса.

Задача №4.2.106 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(p_0=97\) кПа, \(p_3=28,7\) кПа, \(N=3\), \(\frac{V}{V_н}-?\)

Решение задачи:

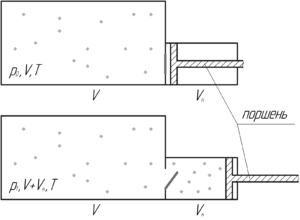Изначально газ занимает объем сосуда \(V\) и оказывает давление \(p_0\). Когда откроется клапан, и поршень переместится на некоторое расстояние (смотрите схему), газ уже будет занимать объем \(\left( {V + {V_н}} \right)\). Если принять, что температура газа остаётся постоянной (\(T=const\)), то можно записать закон Бойля-Мариотта и определить давление газа после одного хода поршня \(p_1\):

\[{p_0}V = {p_1}\left( {V + {V_н}} \right)\]

\[{p_1} = {p_0}\frac{V}{{V + {V_н}}}\;\;\;\;(1)\]

Выполнив аналогичные рассуждения для второго хода поршня, получим:

\[{p_1}V = {p_2}\left( {V + {V_н}} \right)\]

\[{p_2} = {p_1}\frac{V}{{V + {V_н}}}\]

Подставим выражение (1) в последнюю формулу, тогда:

\[{p_2} = {p_0}{\left( {\frac{V}{{V + {V_н}}}} \right)^2}\]

Очевидно, что давление воздуха в сосуде \(p_N\) после \(N\) ходов поршня можно находить по формуле:

\[{p_N} = {p_0}{\left( {\frac{V}{{V + {V_н}}}} \right)^N}\]

Применительно в этой задаче: после трёх ходов поршня (\(N=3\)) давление \(p_3\) можно определить по формуле:

\[{p_3} = {p_0}{\left( {\frac{V}{{V + {V_н}}}} \right)^3}\]

Чтобы найти отношение объема сосуда к объему цилиндра насоса, нужно произвести следующие математические действия:

\[\frac{{{p_3}}}{{{p_0}}} = {\left( {\frac{V}{{V + {V_н}}}} \right)^3}\]

\[\frac{{\sqrt[3]{{{p_3}}}}}{{\sqrt[3]{{{p_0}}}}} = \frac{V}{{V + {V_н}}}\]

\[\frac{{V + {V_н}}}{V} = \frac{{\sqrt[3]{{{p_0}}}}}{{\sqrt[3]{{{p_3}}}}}\]

\[1 + \frac{{{V_н}}}{V} = \frac{{\sqrt[3]{{{p_0}}}}}{{\sqrt[3]{{{p_3}}}}}\]

\[\frac{{{V_н}}}{V} = \frac{{\sqrt[3]{{{p_0}}}}}{{\sqrt[3]{{{p_3}}}}} — 1\]

\[\frac{{{V_н}}}{V} = \frac{{\sqrt[3]{{{p_0}}} — \sqrt[3]{{{p_3}}}}}{{\sqrt[3]{{{p_3}}}}}\]

\[\frac{V}{{{V_н}}} = \frac{{\sqrt[3]{{{p_3}}}}}{{\sqrt[3]{{{p_0}}} — \sqrt[3]{{{p_3}}}}}\]

Посчитаем численный ответ:

\[\frac{V}{{{V_н}}} = \frac{{\sqrt[3]{{28,7 \cdot {{10}^3}}}}}{{\sqrt[3]{{97 \cdot {{10}^3}}} — \sqrt[3]{{28,7 \cdot {{10}^3}}}}} = 2\]

Ответ: 2.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.105 Компрессор всасывает в 1 мин 3 м3 сухого воздуха при температуре 290 К и давлении 100 кПа
4.2.107 В цилиндре длиной 2L=2 м тонкий поршень соединён с днищами пружинами одинаковой
4.2.108 Газ, занимающий при температуре 127 C и давлении 100 кПа объем 2 л, изотермически