В цилиндре под поршнем находится воздух при давлении 0,2 МПа

Условие задачи:

В цилиндре под поршнем находится воздух при давлении 0,2 МПа и температуре 27° C. Какой массы груз нужно положить на поршень после нагревания воздуха в цилиндре до 50° C, чтобы объем воздуха был равен первоначальному? Площадь поршня 30 см².

Задача №4.3.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(p_0=0,2\) МПа, \(t_0=27^\circ\) C, \(t_1=50^\circ\) C, \(S=30\) см², \(V_1=V_0\), \(m-?\)

Решение задачи:

Решающему может показаться, что раз конечный объем равен первоначальному, что имеет место изохорный процесс. Это предположение не верно, поскольку в данном случае объем меняется, и лишь начальное и конечное его значения равны между собой.

На самом деле все намного интереснее, и все действие описывается двумя процессами.

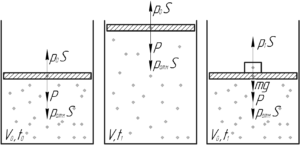
Когда газ начнут нагревать, то этот процесс нагрева является изобарным (\(p=const\)), т.к. вес поршня \(P\) и давление \(p_{атм}S\), оказываемое атмосферой, не меняются.

Далее, когда на поршень поставят груз некоторой массы \(m\), то объем воздуха уменьшится до первоначального. Давайте подумаем, какой это процесс. Он точно не изохорный, поскольку газ сжимается, и не изобарный, так как давление газа будет увеличиваться, пока поршень с грузом не остановится. Но может ли этот процесс быть изотермическим? Давайте обратимся к первому началу термодинамики:

\[Q = \Delta U + A\]

Поршень будет совершать работу над газом, поэтому перепишем выражение в следующем виде (так как \(A=-A_{над}\)):

\[Q = \Delta U – {A_{над}}\]

Нам известно, что теплоту к газу в этом процессе не подводят, т.е. \(Q=0\).

\[\Delta U = {A_1}\]

Получается, что внутренняя энергия газа меняется за счет совершения поршнем работы над ним, а значит меняется и температура!

Видимо автор предполагал, что второй процесс будет идти медленно, что температура не будет меняться. Или просто в условии забыли указать об этом явно (кстати, температуру можно держать постоянной, если лишнее тепло отводить). Если решать задачу, исходя из этого предположения (\(T=const\)), тогда мы сможем получить численный ответ, совпадающий с ответом в сборнике.

Процессы, происходящие с газом, и силы, действующие на поршень, можно увидеть на приведенном рисунке.

Запишем силы, действующие на поршень, в самом начале и самом конце:

\[\left\{ \begin{gathered}
{p_0}S = P + {p_{атм}}S\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
{p_1}S = P + {p_{атм}}S + mg\,\,(2) \hfill \\
\end{gathered} \right.\]

Вычтем из выражения (2) выражение (1) и выразим массу \(m\):

\[m = \frac{{\left( {{p_1} – {p_0}} \right)S}}{g}\]

Запишем объединенный газовый закон (уравнение Клапейрона) для самого начала и самого конца:

\[\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{{p_1}{V_1}}}{{{T_1}}}\]

Так как \(V_1=V_0\), то:

\[\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{{p_1}{V_0}}}{{{T_1}}} \Rightarrow \frac{{{p_0}}}{{{T_0}}} = \frac{{{p_1}}}{{{T_1}}} \Rightarrow \frac{{{p_1}}}{{{p_0}}} = \frac{{{T_1}}}{{{T_0}}}\]

Учитывая, что связь между шкалами температур выражается как \(T=t+273\), то:

\[\frac{{{p_1}}}{{{p_0}}} = \frac{{{t_1} + 273}}{{{t_0} + 273}} \Rightarrow {p_1} = {p_0}\frac{{{t_1} + 273}}{{{t_0} + 273}}\]

Подставим полученное выражение в формулу для нахождения массы груза:

\[m = \frac{{\left( {{p_1} – {p_0}} \right)S}}{g} = \frac{{{p_0}S}}{g}\left( {\frac{{{t_1} + 273}}{{{t_0} + 273}} – 1} \right) = \frac{{{p_0}S}}{g}\left( {\frac{{{t_1} – {t_0}}}{{{t_0} + 273}}} \right)\]

Подставим исходные данные в СИ, получим численный ответ:

\[m = \frac{{0,2 \cdot {{10}^6} \cdot 30 \cdot {{10}^{ – 4}}}}{{10}}\left( {\frac{{50 – 27}}{{27 + 273}}} \right) = 4,6\; кг \]

Ответ: 4,6 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.3.30 Баллон, наполненный воздухом при температуре 273 К и атмосферном
4.3.32 Один конец цилиндрической трубки, длина которой 25 см и радиус 1 см
4.3.33 Расположенная горизонтально, запаянная с обоих концов стеклянная трубка