Решение: В вертикальном закрытом цилиндре находится подвижный поршень

Условие задачи:

В вертикальном закрытом цилиндре находится подвижный поршень, по обе стороны которого находится по одному молю гелия. При равновесии при температуре 320 К объем гелия над поршнем в 4 раза больше объема под поршнем. При какой абсолютной температуре отношение объемов станет равным трем?

Задача №4.3.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu = 1\) моль, \(T=320\) К, \(\frac{V_1}{V_2} = 4\), \(\frac{{V_1^*}}{{V_2^*}} = 3\), \(T^*-?\)

Решение задачи:

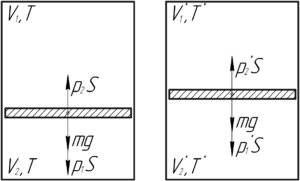Величины без штриха соответствуют моменту до нагревания, со штрихом – после нагревания. Силы, действующие на поршень, показаны на рисунке справа.

Поскольку поршень в обоих случаях находится в равновесии, запишем первый закон Ньютона для этих случаев:

\[\left\{ \begin{gathered}
{p_2}S = mg + {p_1}S \hfill \\
p_2^*S = mg + p_1^*S \hfill \\
\end{gathered} \right.\]

Отнимем из нижнего выражения верхнее, сократим на площадь \(S\) и получим:

\[p_2^* – {p_2} = p_1^* – {p_1}\;\;\;\;(1)\]

Запишем 4 уравнения Клапейрона-Менделеева для каждой части газа до и после нагревания:

\[\left\{ \begin{gathered}
{p_1}{V_1} = \nu RT \hfill \\
{p_2}{V_2} = \nu RT \hfill \\
p_1^*V_1^* = \nu R{T^*} \hfill \\
p_2^*V_2^* = \nu R{T^*} \hfill \\
\end{gathered} \right.\]

Выразим каждое давление и подставим в уравнение (1):

\[\frac{{\nu R{T^*}}}{{V_2^*}} – \frac{{\nu RT}}{{{V_2}}} = \frac{{\nu R{T^*}}}{{V_1^*}} – \frac{{\nu RT}}{{{V_1}}}\]

Сократив на \(\nu R\) будем иметь следующее уравнение:

\[\frac{{{T^*}}}{{V_2^*}} – \frac{T}{{{V_2}}} = \frac{{{T^*}}}{{V_1^*}} – \frac{T}{{{V_1}}}\]

Домножим обе части уравнения на \((V_1 \cdot V_1^*)\), тогда:

\[\frac{{{T^*}{V_1}V_1^*}}{{V_2^*}} – \frac{{T{V_1}V_1^*}}{{{V_2}}} = \frac{{{T^*}{V_1}V_1^*}}{{V_1^*}} – \frac{{T{V_1}V_1^*}}{{{V_1}}}\]

Т.к. по условию \(\frac{V_1}{V_2} = 4\) и \(\frac{{V_1^*}}{{V_2^*}} = 3\), то:

\[3{T^*}{V_1} – 4TV_1^* = {T^*}{V_1} – TV_1^*\]

Поделим обе части уравнения на \(V_1^*\), тогда:

\[3{T^*}\frac{{{V_1}}}{{V_1^*}} – 4T = {T^*}\frac{{{V_1}}}{{V_1^*}} – T\]

\[2{T^*}\frac{{{V_1}}}{{V_1^*}} = 3T\]

В итоге:

\[{T^*} = \frac{{3T}}{2} \cdot \frac{{V_1^*}}{{{V_1}}}\;\;\;\;(2)\]

Осталось найти неизвестное отношение \(\frac{{V_1^*}}{{{V_1}}}\), для чего используем тот факт, что полный объем сосуда не изменятся.

\[\left\{ \begin{gathered}
{V_1} + {V_2} = V \hfill \\
\frac{{{V_1}}}{{{V_2}}} = 4 \hfill \\
\end{gathered} \right. \Rightarrow {V_1} + \frac{{{V_1}}}{4} = V \Rightarrow \frac{{5{V_1}}}{4} = V \Rightarrow {V_1} = \frac{{4V}}{5}\]

\[\left\{ \begin{gathered}
V_1^* + V_2^* = V \hfill \\
\frac{{V_1^*}}{{V_2^*}} = 3 \hfill \\
\end{gathered} \right. \Rightarrow V_1^* + \frac{{V_1^*}}{3} = V \Rightarrow \frac{{4V_1^*}}{3} = V \Rightarrow V_1^* = \frac{{3V}}{4}\]

Так как \({V_1} = \frac{{4V}}{5}\) и \(V_1^* = \frac{{3V}}{4}\), значит:

\[\frac{{V_1^*}}{{{V_1}}} = \frac{{3 \cdot 5}}{{4 \cdot 4}} = \frac{{15}}{{16}}\]

Подставим полученное отношение и исходную температуру в формулу (2):

\[{T^*} = \frac{{3 \cdot 320}}{2} \cdot \frac{{15}}{{16}} = 450 \; К = 177^\circ \; C \]