Условие задачи:

На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной оси вращения лежит груз. Коэффициент трения между грузом и платформой равен 0,2. При какой частоте вращения груз начнет скользить?

Задача №2.4.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=1,15\) м, \(\mu=0,2\), \(\nu-?\)

Решение задачи:

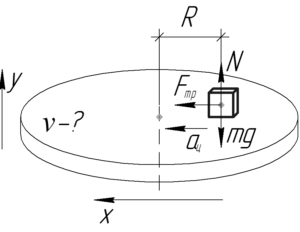На схеме к задаче показана вращающаяся платформа с находящимся на ней грузом, а также система координат. В том момент, когда груз начнет скольжение, на него действуют следующие силы: сила реакции опоры \(N\), сила тяжести \(mg\) и сила трения скольжения \(F_{тр}\). Так как груз покоится вдоль оси \(y\), применим первый закон Ньютона в проекции на эту ось:

\[N = mg\]

Тогда силу трения скольжения можно найти по такому выражению:

\[{F_{тр}} = \mu N = \mu mg\;\;\;\;(1)\]

Запишем второй закон Ньютона в проекции на ось \(x\):

\[{F_{тр}} = m{a_ц}\;\;\;\;(2)\]

Запишем формулу определения центростремительного ускорения через угловую скорость и формулу связи последней с частотой вращения:

\[{a_ц} = {\omega ^2}R\]

\[\omega  = 2\pi \nu \]

Тогда верно следующее:

\[{a_ц} = 4{\pi ^2}{\nu ^2}R\;\;\;\;(3)\]

Подставим выражения (1) и (3) в равенство (2), тогда:

\[\mu mg = 4{\pi ^2}{\nu ^2}mR\]

В конце концов выразим искомую частоту вращения \(\nu\):

\[{\nu ^2} = \frac{{\mu g}}{{4{\pi ^2}R}}\]

\[\nu  = \frac{1}{{2\pi }}\sqrt {\frac{{\mu g}}{R}} \]

Посчитаем численный ответ:

\[\nu  = \frac{1}{{2 \cdot 3,14}}\sqrt {\frac{{0,2 \cdot 10}}{{1,15}}}  = 0,21\; Гц = 12,6\; об/мин\]

Ответ: 12,6 об/мин.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить