Условие задачи:
На каком расстоянии от поверхности шара напряженность электрического поля равномерно заряженной сферической поверхности радиуса 0,2 м уменьшается в 6,25 раз.
Задача №6.2.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=0,2\) м, \(\frac{E_1}{E_2}=6,25\), \(L-?\)
Решение задачи:
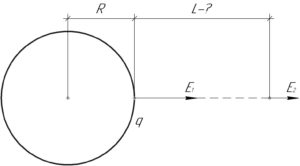 Автор имел в виду, что напряженность поля \(E_2\) на расстоянии \(L\) от поверхности шара (обратите своё внимание на то, что от поверхности, а не центра) уменьшается в 6,25 раз по сравнению с напряженностью поля \(E_1\) на поверхности шара.
Автор имел в виду, что напряженность поля \(E_2\) на расстоянии \(L\) от поверхности шара (обратите своё внимание на то, что от поверхности, а не центра) уменьшается в 6,25 раз по сравнению с напряженностью поля \(E_1\) на поверхности шара.
Модули указанных напряженностей можно найти по таким формулам:
\[\left\{ \begin{gathered}
{E_1} = \frac{{kq}}{{{R^2}}} \hfill \\
{E_2} = \frac{{kq}}{{{{\left( {R + L} \right)}^2}}} \hfill \\
\end{gathered} \right.\]
Поделим верхнее равенство на нижнее, тогда получим:
\[\frac{{{E_1}}}{{{E_2}}} = \frac{{{{\left( {R + L} \right)}^2}}}{{{R^2}}}\]
По условию \(\frac{E_1}{E_2}=6,25\), поэтому:
\[\frac{{{{\left( {R + L} \right)}^2}}}{{{R^2}}} = 6,25\]
\[\frac{{R + L}}{R} = 2,5\]
\[R + L = 2,5R\]
\[L = 1,5R\]
Посчитаем ответ:
\[L = 1,5 \cdot 0,2 = 0,3\;м\]
Ответ: 0,3 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.54 Точечный положительный заряд создаёт на расстоянии 10 см электрическое поле
6.2.56 Равномерно заряженный проводящий шар радиуса 5 см создаёт на расстоянии 10 см
6.2.57 Проводящий шар радиуса R заряжен зарядом q. Найти напряженность поля в точке

 icodepro.ru
icodepro.ru