Условие задачи:
На какой угол повернется отраженный от зеркала солнечный луч при повороте зеркала на угол 30°?
Задача №10.1.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\gamma-?\)
Решение задачи:
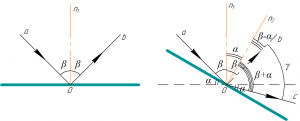 Пусть солнечный луч падает на зеркало под некоторым углом \(\beta\) к нормали (см. левую часть рисунка к задаче). Напомним, что угол падения равен углу отражения, поэтому лучи \(a\) и \(b\) расположены под одинаковым углом к нормали \(n_1\).
Пусть солнечный луч падает на зеркало под некоторым углом \(\beta\) к нормали (см. левую часть рисунка к задаче). Напомним, что угол падения равен углу отражения, поэтому лучи \(a\) и \(b\) расположены под одинаковым углом к нормали \(n_1\).
Зеркало поворачивают на угол \(\alpha\) (мы поворачивали по часовой стрелке, см. правую часть рисунка). При повороте зеркала изменится положение нормали к зеркалу, она также повернется на угол \(\alpha\) (на рисунке этот угол показан как угол между начальным положением нормали \(n_1\) и конечным положением нормали \(n_2\)). Угол падения солнечного луча теперь становится равным \(\left(\beta + \alpha\right)\), новое положение отраженного луча на рисунке показано лучом \(c\).
Чтобы найти искомый угол \(\gamma\), нужно также найти угол между новым положением нормали \(n_2\) и старым положением отраженного луча \(b\). Из рисунка прекрасно видно, что этот угол равен \(\left(\beta — \alpha\right)\). Тогда из рисунка очевидно, что искомый угол \(\gamma\) равен:
\[\gamma = \beta + \alpha — \left( {\beta — \alpha } \right)\]
\[\gamma = 2\alpha \]
Численный ответ равен:
\[\gamma = 2 \cdot 30^\circ = 60^\circ \]
Ответ: 60°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.37 При нормальном падении белого света на дифракционную решетку зеленая линия
10.1.2 Предмет находился на расстоянии 20 см от плоского зеркала. Затем его отодвинули на 10 см
10.1.3 В плоскости экрана находится источник света, испускающий узкий пучок лучей под углом

 icodepro.ru
icodepro.ru