Условие задачи:
На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение в вертикальной плоскости с постоянной угловой скоростью 10 рад/с. Ось вращения проходит через конец стержня. Какова при таком вращении сила, действующая на стержень со стороны груза в верхней точке траектории?
Задача №2.4.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=10\) см, \(m=0,4\) кг, \(\omega=10\) рад/с, \(F-?\)
Решение задачи:
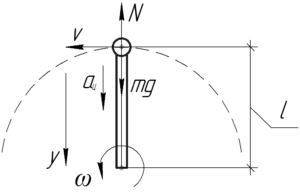 Искомая сила \(F\) равна по величине, но противоположна по направлению силе реакции \(N\) согласно третьему закону Ньютона.
Искомая сила \(F\) равна по величине, но противоположна по направлению силе реакции \(N\) согласно третьему закону Ньютона.
\[F = N\;\;\;\;(1)\]
Тогда запишем в проекции на ось \(y\) второй закон Ньютона:
\[mg — N = m{a_ц}\]
Также вспомним формулу нахождения центростремительного ускорения \(a_ц\) через угловую скорость \(\omega\).
\[{a_ц} = {\omega ^2}l\]
\[mg — N = m{\omega ^2}l\]
\[N = m\left( {g — {\omega ^2}l} \right)\]
Учитывая (1), получаем решение этой задачи в общем виде:
\[F = m\left( {g — {\omega ^2}l} \right)\]
Переведем длину стержня в метры, а далее займемся расчетом численного ответа.
\[10\; см = \frac{{10}}{{100}}\; м = 0,1\; м\]
\[F = 0,4 \cdot \left( {10 — {{10}^2} \cdot 0,1} \right) = 0\; Н\]
Ответ: 0 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного
2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси

 icodepro.ru
icodepro.ru