Условие задачи:

На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести нить от положения равновесия, чтобы при последующих качаниях максимальная сила натяжения нити была в 1,5 раза больше минимальной?

Задача №2.4.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(T_{max}=1,5T_{min}\), \(\alpha-?\)

Решение задачи:

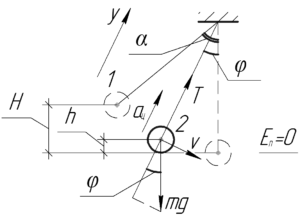Давайте решим эту задачу в общем виде: мы докажем, что минимальное значение силы натяжения нити наблюдается в крайнем положении шарика, а максимальное — в момент прохождения им положения равновесия. Примем длину нити равной \(l\). Пусть изначально шарик на нити отводят так, что нить составляет угол \(\alpha\) с вертикалью (положение 1). Нам же необходимо найти силу натяжения нити \(T\), когда нить отклонена на угол \(\varphi\), очевидно меньший, чем \(\alpha\) (положение 2).

Первым делом применим второй закон Ньютона в проекции на ось \(y\) для положения 2 (смотрите схему):

\[T — mg \cdot \cos \varphi  = m{a_ц}\]

Пусть в этой точке скорость шарика равна \(\upsilon\), тогда центростремительное ускорение \(a_ц\) равно:

\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]

\[T — mg \cdot \cos \varphi  = m\frac{{{\upsilon ^2}}}{l}\]

\[T = m\left( {g \cdot \cos \varphi  + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(1)\]

На шарик не действуют неконсервативные силы, поэтому запишем закон сохранения энергии (ЗСЭ) для положений 1 и 2.

\[mgH = mgh + \frac{{m{\upsilon ^2}}}{2}\]

Необходимо выразить неизвестные высоты \(H\) и \(h\) через длину нити \(l\) и углы \(\alpha\) и \(\varphi\). На схеме видно, что:

\[H = l\left( {1 — \cos \alpha } \right)\]

\[h = l\left( {1 — \cos \varphi } \right)\]

Тогда ЗСЭ примет вид:

\[mgl\left( {1 — \cos \alpha } \right) = mgl\left( {1 — \cos \varphi } \right) + \frac{{m{\upsilon ^2}}}{2}\]

\[mgl\left( {\cos \varphi  — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]

\[{\upsilon ^2} = 2gl\left( {\cos \varphi  — \cos \alpha } \right)\]

Последнее выражение подставим в (1), тогда:

\[T = m\left( {g \cdot \cos \varphi  + \frac{{2gl\left( {\cos \varphi  — \cos \alpha } \right)}}{l}} \right)\]

\[T = mg\left( {3\cos \varphi  — 2\cos \alpha } \right)\]

Поработаем над полученной формулой. Когда сила натяжения примет минимальное значение? По формуле видно, что когда угол \(\varphi\) равен углу \(\alpha\). Это крайнее положение шарика, когда его скорость равна нулю.

\[{T_{min}} = mg\left( {3\cos \alpha  — 2\cos \alpha } \right)\]

\[{T_{min}} = mg \cdot \cos \alpha \;\;\;\;(2)\]

Когда же сила натяжения станет максимальной? Это произойдет тогда, когда косинус угла \(\varphi\) будет равен единице, т.е. сам угол \(\varphi\) равен нулю. Это положение равновесия шарика, когда его скорость максимальна.

\[{T_{max}} = mg\left( {3 — 2\cos \alpha } \right)\;\;\;\;(3)\]

По условию отношение максимального значения силы натяжения к минимальному равно 1,5. Поэтому поделим выражения (3) и (2) друг на друга, получим:

\[\frac{{3 — 2\cos \alpha }}{{\cos \alpha }} = \frac{3}{2}\]

\[3\cos \alpha  = 6 — 4\cos \alpha \]

\[7\cos \alpha  = 6\]

\[\alpha  = \arccos \left( {\frac{6}{7}} \right) = 31^\circ  \approx \frac{\pi }{6}\]

Ответ: \(\frac{\pi }{6}\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной