Условие задачи:
На нити подвешен заряженный шар массой 300 г. Когда к нему поднесли снизу на расстояние 40 см заряженный таким же зарядом шар радиусом 2 см, то сила натяжения нити уменьшилась в 4 раза. Определить поверхностную плотность электрического заряда на поднесённом шаре.
Задача №6.1.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=300\) г, \(R=40\) см, \(r=2\) см, \(T=\frac{T_0}{4}\), \(\sigma-?\)
Решение задачи:
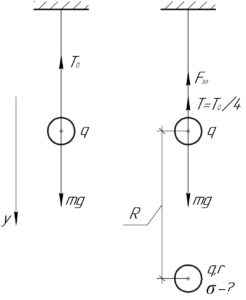 Изначально шар, висящий на нити, находился в равновесии под действием двух сил: силы тяжести \(mg\) и силы натяжения нити \(T\). Запишем первый закон Ньютона в проекции на ось \(y\) (смотрите левую часть схемы):
Изначально шар, висящий на нити, находился в равновесии под действием двух сил: силы тяжести \(mg\) и силы натяжения нити \(T\). Запишем первый закон Ньютона в проекции на ось \(y\) (смотрите левую часть схемы):
\[mg — {T_0} = 0\;\;\;\;(1)\]
После того, как снизу поднесут шарик радиусом \(r\) на расстояние \(R\) с таким же зарядом \(q\), сила натяжения уменьшится, поскольку появится ещё кулоновская сила отталкивания \(F_{эл}\). Также запишем первый закон Ньютона в проекции на ось \(y\) (смотрите правую часть схемы):
\[mg — T — {F_{эл}} = 0\]
По условию задачи сила натяжения нити уменьшилась в 4 раза (\(T=\frac{T_0}{4}\)), поэтому:
\[mg — \frac{{{T_0}}}{4} — {F_{эл}} = 0\]
Умножим обе части уравнения на 4, тогда:
\[4mg — {T_0} — 4{F_{эл}} = 0\;\;\;\;(2)\]
Из (2) вычтем (1), тогда получим:
\[3mg = 4{F_{эл}}\;\;\;\;(3)\]
Так как заряды обоих шаров одинаковы и равны \(q\) (как на поднесённом шаре), расстояние между центрами шаров равно \(R\), то силу кулоновского отталкивания найдём по такой формуле:
\[{F_{эл}} = \frac{{k{q^2}}}{{{R^2}}}\;\;\;\;(4)\]
Коэффициент пропорциональности \(k\) равен 9·109 Н·м2/Кл2.
Поскольку заряд \(q\) равномерно распределен на поднесённом шаре, то справедливо:
\[q = \sigma S\;\;\;\;(5)\]
Площадь поверхности шара \(S\) можно определить по такой формуле из математики:
\[S = 4\pi {r^2}\;\;\;\;(6)\]
Тогда формула (4) с учётом (5) и (6) примет такой вид:
\[{F_{эл}} = \frac{{16k{\sigma ^2}{\pi ^2}{r^4}}}{{{R^2}}}\]
Полученное выражение подставим в равенство (3), тогда:
\[3mg = \frac{{64k{\sigma ^2}{\pi ^2}{r^4}}}{{{R^2}}}\]
В итоге искомую поверхностную плотность электрического заряда на поднесённом шаре \(\sigma\) можно найти по формуле:
\[\sigma = \frac{R}{{8\pi {r^2}}}\sqrt {\frac{{3mg}}{k}} \]
Посчитаем численный ответ:
\[\sigma = \frac{{0,4}}{{8 \cdot 3,14 \cdot {{0,02}^2}}}\sqrt {\frac{{3 \cdot 0,3 \cdot 10}}{{9 \cdot {{10}^9}}}} = 0,00126\;Кл/м^2 = 1,26\;мКл/м^2\]
Ответ: 1,26 мКл/м2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.1.19 Два заряда по 25 нКл каждый, расположенные на расстоянии 0,24 м друг от друга
6.1.21 На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл
6.1.22 Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах

 icodepro.ru
icodepro.ru
найдена ошибка в решении. До корня получается число 39,8. Под корнем получаем после всех сокращений 10^-8. Выводим из под корня и умножаем на число. Должно получиться 39,8*10^-4 Кл/м^2 или 4 мКл/м^2.
1,26 получается если не делить на число пи=3,14
Под корнем получится 10-9, поэтому в решении всё правильно