Условие задачи:
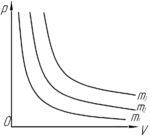 На рисунке изображены гиперболы для трех идеальных газов с разными массами (\(m_1\), \(m_2\), \(m_3\)) и одинаковой молярной массой, находящихся при одинаковой температуре. Каково соотношение между массами этих газов? Рисунок, приведенный в условии к задаче, изображен справа.
На рисунке изображены гиперболы для трех идеальных газов с разными массами (\(m_1\), \(m_2\), \(m_3\)) и одинаковой молярной массой, находящихся при одинаковой температуре. Каково соотношение между массами этих газов? Рисунок, приведенный в условии к задаче, изображен справа.
Задача №4.3.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
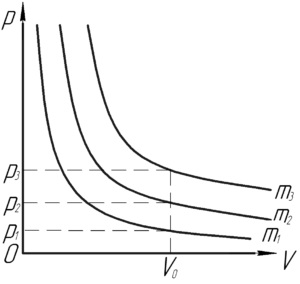 Подобная задача уже была решена на сайте. Проведем вертикаль, пересекающую все графики — так мы рассматриваем газы при одинаковом объеме.
Подобная задача уже была решена на сайте. Проведем вертикаль, пересекающую все графики — так мы рассматриваем газы при одинаковом объеме.
Теперь запишем уравнение Клапейрона-Менделеева:
\[pV = \frac{m}{\mu }RT\]
Выразим массу газа:
\[m = \frac{{pV\mu }}{{RT}} = pV\frac{\mu }{{RT}}\]
Множитель \(\frac{\mu }{{RT}}\) остается всегда постоянным, согласно условию. Произведение \(pV\) — это не что иное, как площадь прямоугольника, образованного из прямых, проведенных через точку пересечения нашей вертикали с конкретным графиком параллельно осям, и самих осей. Получается, где эта площадь больше, там и больше масса газа, поэтому:
\[{p_1}{V_0} < {p_2}{V_0} < {p_3}{V_0}\]
\[{m_1} < {m_2} < {m_3}\]
Ответ: \({m_1} < {m_2} < {m_3}\)
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.3.42 На рисунке изображены гиперболы для трех идеальных газов с одинаковыми массами
4.3.44 Постоянную массу идеального газа переводят из состояния 1
4.3.45 Горизонтально расположенный закрытый цилиндрический сосуд длины

 icodepro.ru
icodepro.ru