icodepro.ruУсловие задачи:
На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень с подвешенным на нити шариком массой 2 г. Найти силу натяжения нити, если плоскость образует с горизонтом угол 60°.
Задача №2.3.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=2\) г, \(\alpha=60^\circ\), \(T-?\)
Решение задачи:
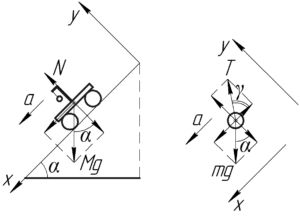Покажем на схеме тележку со стержнем и шариком. Введем оси координат: ось \(y\) перпендикулярно наклонной плоскости, а ось \(x\) — вдоль неё. Теперь рассмотрим систему «тележка — шарик». На неё действуют две внешние силы: сила тяжести и сила реакции опоры. Так как эта система движется ускоренно вдоль оси \(x\), то запишем теорему о движении центра масс в проекции на эту ось:
\[Mg \cdot \sin \alpha = Ma\]
Здесь \(M\) — суммарная масса системы.
\[a = g \cdot \sin \alpha \]
Каждая точка этой системы движется поступательно с этим ускорением!
Теперь рассмотрим шарик отдельно. На него действует сила тяжести, сила натяжения нити. Предположим, что нить составляет угол \(\gamma\) с осью \(x\), значит и сила натяжения \(T\) направлена также. Запишем второй закон Ньютона в проекции на ось \(x\):
\[mg \cdot \sin \alpha — T \cdot \cos \gamma = ma\;\;\;\;(1)\]
Также применим первый закон Ньютона в проекции на ось \(y\):
\[T \cdot \sin \gamma = mg \cdot \cos \alpha \;\;\;\;(2)\]
Подставим в равенство (1) ранее определенное ускорение:
\[mg \cdot \sin \alpha — T \cdot \cos \gamma = mg \cdot \sin \alpha \]
\[T \cdot \cos \gamma = 0\]
Так как сила натяжения точно не равна нулю, значит равен нулю косинус угла \(\gamma\).
\[\cos \gamma = 0\]
\[\gamma = 90^\circ \]
Получается, что нить направлена перпендикулярно оси \(x\) (как она и изображена на левой части схемы). Тогда можно определить искомую силу \(T\) из равенства (2):
\[T = mg \cdot \cos \alpha \]
Переведем массу шарика в систему СИ:
\[2\; г = \frac{2}{{1000}}\; кг = 0,002\; кг\]
Посчитаем ответ:
\[T = 0,002 \cdot 10 \cdot \cos 60^\circ = 0,01\; Н\]
Ответ: 0,01 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
Ну, вот эта нестрогость и смущает… Слегка. «Падение с 3-х метровой высоты и скольжение с горки такой же высоты есть одно и то же.» Если с одним и тем же ускорением, то, пожалуй, да. В простом падении равнодействующая всех сил просто сила тяжести (ну без сопротивления воздуха). А в скольжении равнодействующая сумма силы тяжести, реакции опоры и силы трения (если она есть). Если они равны, то какая разница какова природа силы, сообщающей ускорение?
И с состоянием невесомости то же самое — это не очень корректно, но всё же — почему нельзя рассматривать состояние невесомости вдоль какой-то оси? Невеcом по X и имеет вес по Y?
А направление ускорения Вас не интересует?
Смысл понятия невесомости теряется, поэтому и нельзя. Невесомость — состояние тела, когда оно не оказывает воздействия на опору или подвес, т.е. полная реакция опоры или сила натяжения равна нулю. Подчеркиваю — именно полная реакция (или сила натяжения). Поэтому и нет смысла рассматривать невесомость по осям.
Может это не очень строго, но…
Рассмотрим силы в проекциях на оси x и y. Вдоль оси y шарику (как и всей системе тележка-шарик) ничего не мешает падать. Соответственно шарик находится в состоянии невесомости (по аналогии с падающим лифтом). Вдоль оси y на шарик действуют две силы — проекция силы натяжения на ось y (она же сама сила натяжения, так как перпендикулярная составляющая этой силы равна нулю — там же невесомость) и проекция силы тяжести.
Отсюда T = m*g*cos(\alpha).
А проекция силы тяжести m*g*sin(\alpha) ничем не уравновешена и именно она двигает систему с ускорением a = g*sin(\alpha).
На мой взгляд, заявление, что «T точно не равно нулю» не очень убедительно…
При m=0, или g=0, или \alpha=\pi/2 как раз T=0. Почему в нашем случае не равно? Оно не равно, конечно, но это стоит как-то объяснить. Например формулой (2). Из неё как раз следует, что T=0 только при равенстве нулю m, g или cos(\alpha)
Нет, такие рассуждения мне совсем не нравятся.
«Вдоль оси y шарику (как и всей системе тележка-шарик) ничего не мешает падать» — Вы уверены? Тогда для Вас падение с 3-х метровой высоты и скольжение с горки такой же высоты есть одно и то же. Почему Вы такое движение называете падением?
«Шарик находится в состоянии невесомости (по аналогии с падающим лифтом)» — Вы не понимаете, что такое невесомость, более того, если Вы получаете ответ, отличный от нуля, то Вы сами себе и противоречите. Не нужно проводить таких аналогий.
«На мой взгляд, заявление, что «T точно не равно нулю» не очень убедительно» — убедительно, в противном случае шарик действительно падал, а не двигался с тележкой. Более того, из (2) видно, что сила натяжения может быть равна нулю только при ?, равном 90 градусов.