Решение: Над одним молем идеального газа совершают цикл, показанный на рисунке

Условие задачи:

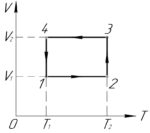Над одним молем идеального газа совершают цикл, показанный на рисунке. Определить КПД цикла, если работа газа на участке 2-3 равна 2 кДж, а на участке 1-4 равна 1,5 кДж. \(T_1=300\) К, \(T_2=2T_1\).

Задача №5.5.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=1\) моль, \(A_{23}=2\) кДж, \(A_{14}=1,5\) кДж, \(T_1=300\) К, \(T_2=2T_1\), \(\eta-?\)

Решение задачи:

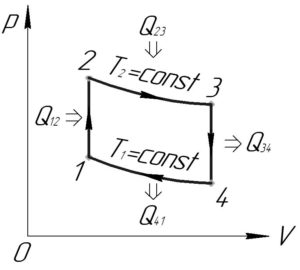Изобразим проводимый над газом цикл в координатах p-V (смотрите схему к решению).

Коэффициент полезного действия цикла \(\eta\) будем определять по следующей формуле:

\[\eta = \frac{A}{{{Q_н}}}\;\;\;\;(1)\]

Из графика цикла в координатах p-V видно, что работа газа в процессах 1-2 и 3-4 равна нулю (так площадь фигур под графиками этих процессов равна нулю). Тогда работа цикла \(A\) равна:

\[A = {A_{23}} + {A_{41}}\]

Понятно, что \(A_{41} = — A_{14}\), поэтому:

\[A = {A_{23}} — {A_{14}}\;\;\;\;(2)\]

Чтобы найти количество теплоты \(Q_н\), нужно найти все процессы в цикле, в которых тепло подводилось к газу. Для это нам понадобится первый закон термодинамики:

\[Q = \Delta U + A\;\;\;\;(3)\]

Также изменение внутренней энергии газа \(\Delta U\) следует искать по формуле (будем считать, что газ одноатомный, иначе задачу решить не получится):

\[\Delta U = \frac{3}{2}\nu R\Delta T\;\;\;\;(4)\]

Рассмотрим изохорный процесс 1-2 (\(V=const\)). Работа газа \(A_{12}\) в этом процессе равна нулю. Тогда по формулам (3) и (4) количество теплоты \(Q_{12}\) равно:

\[{Q_{12}} = \frac{3}{2}\nu R\Delta {T_{12}}\;\;\;\;(5)\]

Так как в изохорном процессе 1-2 давление увеличивается, значит по закону Шарля увеличивается и температура (то есть \(\Delta T_{12}>0\)). Поэтому согласно формуле (5) можно сделать вывод, что \(Q_{12}>0\), то есть в этом процессе тепло подводится к газу. Также:

\[{Q_{12}} = \frac{3}{2}\nu R\left( {{T_2} — {T_1}} \right)\]

В условии говорится, что \(T_2=2T_1\), поэтому:

\[{Q_{12}} = \frac{3}{2}\nu R\left( {2{T_1} — {T_1}} \right)\]

\[{Q_{12}} = \frac{3}{2}\nu R{T_1}\;\;\;\;(6)\]

Если Вы проведёте аналогичные рассуждения для другого изохорного процесса 3-4, то придёте к выводу, что \(Q_{34}<0\), то есть в этом процессе теплота отводится от газа.

Теперь рассмотрим изотермический процесс 2-3 (\(T=const\)). Так как температура газа в этом процессе постоянна, значит изменение внутренней энергии газа \(\Delta U_{23}\) по формуле (4) равно нулю. По формулам (3) и (4) количество теплоты \(Q_{23}\) равно:

\[{Q_{23}} = {A_{23}}\;\;\;\;(7)\]

Так как газ в этом процессе расширяется, то \(A_{23}>0\) (также это понятно из условия, поскольку дано численное значение \(A_{23}\)), значит согласно формуле (7) в процессе 2-3 теплота подводилась к газу.

Проведя аналогичные рассуждения для другого изотермического процесса 4-1, Вы придёте к выводу, что \(Q_{41}<0\), то есть в этом процессе теплота отводится от газа.

Получается, что теплота к газу подводилась только в процессах 1-2 и 2-3, поэтому количество теплоты \(Q_н\) равно:

\[{Q_н} = {Q_{12}} + {Q_{23}}\]

Учитывая формулы (6) и (7), получим:

\[{Q_н} = \frac{3}{2}\nu R{T_1} + {A_{23}}\;\;\;\;(8)\]

Чтобы получить окончательную формулу для расчёта КПД \(\eta\), подставим в формулу (1) выражения (2) и (8):

\[\eta = \frac{{{A_{23}} — {A_{14}}}}{{\frac{3}{2}\nu R{T_1} + {A_{23}}}}\]

Посчитаем численный ответ:

\[\eta = \frac{{2000 — 1500}}{{\frac{3}{2} \cdot 1 \cdot 8,31 \cdot 300 + 2000}} = 0,0871 = 8,71\% \]