Условие задачи:
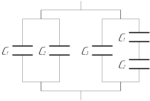 Найти общую электроемкость соединенных по схеме конденсаторов, если \(C_1=2\) мкФ, \(C_2=3\) мкФ, \(C_3=1\) мкФ.
Найти общую электроемкость соединенных по схеме конденсаторов, если \(C_1=2\) мкФ, \(C_2=3\) мкФ, \(C_3=1\) мкФ.
Задача №6.4.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=2\) мкФ, \(C_2=3\) мкФ, \(C_3=1\) мкФ, \(C-?\)
Решение задачи:
В крайней правой ветви два конденсатора с емкостями \(C_1\) и \(C_2\) соединены последовательно, заменим их эквивалентной емкостью \(C_4\), которую можно найти следующим образом:
\[\frac{1}{{{C_4}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}\]
\[\frac{1}{{{C_4}}} = \frac{{{C_1} + {C_2}}}{{{C_1}{C_2}}}\]
\[{C_4} = \frac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}\;\;\;\;(1)\]
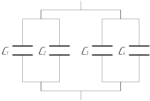 Тогда схема примет такой простой вид (смотрите схему справа). Она представляет собой четыре соединенных параллельно конденсатора, поэтому общую электроемкость \(C\) можно найти по формуле:
Тогда схема примет такой простой вид (смотрите схему справа). Она представляет собой четыре соединенных параллельно конденсатора, поэтому общую электроемкость \(C\) можно найти по формуле:
\[C = {C_1} + {C_2} + {C_3} + {C_4}\]
Учитывая (1), окончательно получим:
\[C = {C_1} + {C_2} + {C_3} + \frac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}\]
Посчитаем численный ответ:
\[C = 2 \cdot {10^{ — 6}} + 3 \cdot {10^{ — 6}} + 1 \cdot {10^{ — 6}} + \frac{{2 \cdot {{10}^{ — 6}} \cdot 3 \cdot {{10}^{ — 6}}}}{{2 \cdot {{10}^{ — 6}} + 3 \cdot {{10}^{ — 6}}}} = 7,2 \cdot {10^{ — 6}}\;Ф = 7,2\;мкФ\]
Ответ: 7,2 мкФ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.41 Конденсатор, заряженный до разности потенциалов 20 В, соединили параллельно разноименными
6.4.43 Определить электроемкость батареи конденсаторов, изображенной на рисунке
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B

 icodepro.ru
icodepro.ru
Здравствуйте, прошу прощения, разве с1 и с2 не соединены параллельно, вообще не понимаю!