icodepro.ruУсловие задачи:
Небольшое тело скользит с вершины полусферы вниз. На какой высоте \(h\) от вершины полусферы тело оторвется от поверхности сферы радиусом \(R\)? Трением пренебречь.
Задача №2.8.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R\), \(h-?\)
Решение задачи:
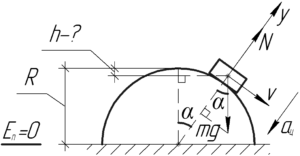Когда тело оторвется от полусферы, то сила реакции опоры \(N\) станет равной нулю. Допустим это произойдет в момент, когда прямая, соединяющая тело и центр полусферы (смотри схему), составляет с вертикалью угол \(\alpha\). Запишем второй закон Ньютона в проекции на ось \(y\), которая совпадает с упомянутой прямой.
\[- mg \cdot \cos \alpha + N = – m{a_ц}\]
Учитывая, что центростремительное ускорение \(a_ц\) равно \(\frac{{{\upsilon ^2}}}{R}\), то:
\[mg \cdot \cos \alpha – N = m\frac{{{\upsilon ^2}}}{R}\]
Выше уже было сказано, что \(N=0\), поэтому:
\[mg \cdot \cos \alpha = m\frac{{{\upsilon ^2}}}{R}\]
\[{\upsilon ^2} = gR \cdot \cos \alpha \;\;\;\;(1)\]
Так как трением можно пренебречь, то воспользуемся законом сохранения энергии:
\[mgR = \frac{{m{\upsilon ^2}}}{2} + mgR \cdot \cos \alpha \]
\[{\upsilon ^2} = 2gR\left( {1 – \cos \alpha } \right)\;\;\;\;(2)\]
Так как левые части в равенствах (1) и (2) равны, то приравняем их правые части:
\[gR \cdot \cos \alpha = 2gR\left( {1 – \cos \alpha } \right)\]
\[\cos \alpha = 2 – 2\cos \alpha \]
\[\cos \alpha = \frac{2}{3}\]
Искомую высоту \(h\) можно найти по формуле (смотри схему):
\[h = R – R \cdot \cos \alpha = R\left( {1 – \cos \alpha } \right)\]
\[h = R\left( {1 – \frac{2}{3}} \right) = \frac{R}{3}\]
Ответ: \(\frac{R}{3}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
2.8.48 Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
почему проекции сил на ось y равны: -mgcosa+N=-maц, если N = m(gcosa+ац). В вашем же случае получается, что N=mgcosa. Вес тела же будет равен m(gcosa+ац), разве нет?
перечитал определение веса , понял что действительно n = -mgcosa. Вопрос снят
Изменится ли ответ, если тело будет скатываться со сферы, а не с полусферы?
А если есть сила трения с коофицентом u(мю) , то как ее учитывать?
Условие отрыва тела от полусферы (второй закон Ньютона в проекции на ось \(y\)) не изменится, а вот в законе сохранения энергии необходимо учесть работу силы трения. Учитывая, что модуль силы трения меняется по мере движения тела по полусфере, то без интегралов Вы здесь обойтись не сможете, а это уже выходит за рамки школьного курса
Мне кажется, там ошибка: в конце, чтобы найти высоту, надо было просто вычислить R*cos(a), потому что просят же найти высоту отрыва не от вершины, а от основания. В этом случае показан ответ от вершины
Ошибки нет, в условии сказано найти на какой высоте от вершины полусферы тело оторвется от полусферы
можете объяснить откуда вы взяли формулу с высотой? как она выводиться или как её получить?
Смотрите на рисунок. Искомую высоту \(h\) (она показана на рисунке) можно найти, если вычесть из радиуса \(R\) полусферы прилежащий к углу \(\alpha\) катет прямоугольного треугольника, образованного центром полусферы, центром тяжести тела и точкой пересечения вертикали, проведенной из центра полусферы, и горизонтали, проведенной из центра тяжести тела (на рисунке там показан прямой угол). Указанный катет равен \(R\cos \alpha \). Поэтому:\[h = R – R\cos \alpha \]\[h = R\left( {1 – \cos \alpha } \right)\]
Почему касательное ускорение равно 0?
Ведь во 2 законе Ньютона участвует полное ускорение, т.е. векторная сумма касательного и центростремительного ускорений?
Нет, оно не равно нулю (собственно говоря, я об этом в решении не писал).
Да, в общем случае в записи второго закона Ньютона участвует полное ускорение, но при решении задачи я использовал этот закон в проекции на ось \(y\), перпендикулярной направлению скорости. Поэтому у меня в записи второго закона Ньютона не полное ускорение, а нормальное (т.е. центростремительное).
Объясните закон сохранения энергии
Я не понял финальную часть, где мы находим высоту через косинус. Почему не просто R*cos(a), вы же сами когда записывали закон сохранении энергии потенциальная энергия mgh=mgRcos(a) писали
Посмотрите на рисунок, чтобы понять, что за расстояние \(h\) мы находим (это высота от вершины полусферы, как написано в условии). Поэтому его нужно искать по формуле, указанной в решении, а не так, как предлагаете Вы.
И в законе сохранения энергии у меня нет этой высоты \(h\), Вы ошиблись.
а если сфера тоже может скользить?
Если сфера скользит, то в законе сохранения энергии нужно будет учесть кинетическую энергию полусферы. Скорость полусферы можно найти из закона сохранения импульса.