Условие задачи:
Однородный конус массой 48 кг плавает в воде вершиной вниз. Определить высоту выступающей над водой части конуса, если высота конуса равна 1 м, а площадь основания — 0,25 м2.
Задача №3.3.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=48\) кг, \(H=1\) м, \(S=0,25\) м2, \(\Delta h-?\)
Решение задачи:
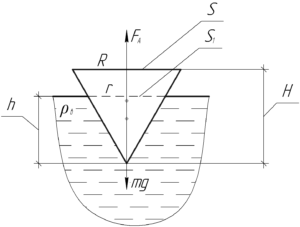 Так как конус плавает, запишем условие плавания тел:
Так как конус плавает, запишем условие плавания тел:
\[mg = {F_А}\]
Распишем по известной формуле выталкивающую силу \(F_А\) в правой части равенства:
\[mg = {\rho _в}g{V_п}\]
\[m = {\rho _в}{V_п}\]
В этой формуле \(V_п\) — объем части конуса, погруженной в воду, его можно найти по следующей формуле:
\[{V_п} = \frac{1}{3}{S_1}h \]
Тогда:
\[m = {\rho _в} \cdot \frac{1}{3}{S_1}h\;\;\;\;(1)\]
Из подобия треугольников (что хорошо видно на схеме) следует:
\[\frac{r}{R} = \frac{h}{H}\]
Возведём обе части равенства в квадрат. Также числитель и знаменатель дроби в левой части равенства домножим на \(\pi\):
\[\frac{{\pi {r^2}}}{{\pi {R^2}}} = {\left( {\frac{h}{H}} \right)^2}\]
Так как \(S_1 = \pi r^2\) и \(S = \pi R^2\), то:
\[\frac{{{S_1}}}{S} = {\left( {\frac{h}{H}} \right)^2}\]
\[{S_1} = S\frac{{{h^2}}}{{{H^2}}}\]
Подставим полученное выражение в формулу (1):
\[m = \frac{1}{3}{\rho _в}S\frac{{{h^3}}}{{{H^2}}}\]
\[h = \sqrt[3]{{\frac{{3m{H^2}}}{{{\rho _в}S}}}}\]
Искомую высоту выступающей над водой части конуса \(\Delta h\), очевидно, определим из выражения:
\[\Delta h = H — h\]
\[\Delta h = H — \sqrt[3]{{\frac{{3m{H^2}}}{{{\rho _в}S}}}}\]
Посчитаем численный ответ:
\[\Delta h = 1 — \sqrt[3]{{\frac{{3 \cdot 48 \cdot {1^2}}}{{1000 \cdot 0,25}}}} = 0,17\;м\]
Ответ: 0,17 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.42 В цилиндрическом сосуде диаметром 50 см плавает льдинка объемом 12 дм3. В льдинку
3.3.44 Цилиндр плавает в вертикальном положении в сосуде с водой. В сосуд подливают более
3.3.45 Шарик от настольного тенниса диаметром 4 см и массой 8 г удерживается под водой

 icodepro.ru
icodepro.ru
Здравствуйте. Спасибо за подробное описание расчета. Но передо мной стоит более сложная задача. Собираюсь варить из ПНД плот с деревянным настилом размером 6 х 4 . И планирую сами баллоны делать не из труб, а в виде призм длиной по 3 метра 4 штуки скрепленных жестко между собой деревянными брусьями. Так как считаю, что такая форма будет иметь дифферинцируемую выталкивающую силу при увеличении нагрузки на плот. Из расчета, что на него зайдут 4 человека по 80 кг и высота от настила до поверхности воды будет 17-20 см. То есть он не должен быть высоко от воды , как это происходит с понтонами на трубах или бочках. Поможете с расчетом размеров сторон призм?
(Объяснение из одного сайта) «Конус является симметричной фигурой, и считается, что заряд равномерно растекается по нему.» Это верное утверждение? Почему?
Распределение заряда будет равномерным, если кривизна поверхности во всех точках будет одинаковой — такое имеет место для плоской, цилиндрической и сферической поверхностей. У конуса кривизна в различных точках разная, поэтому распределение зарядов оказывается неравномерным. Заряд будет стремиться скапливаться у вершины конуса.
То есть у куба распределение заряда будет равномерным?
Нет, у куба заряд будет стремиться скапливаться на вершинах (потому что там малая кривизна поверхности).