Условие задачи:

Однородный стержень длиной 1 м и площадью сечения 1 см² плавает в вертикальном положении, погружаясь в воду на 80% длины. Какую минимальную работу нужно совершить, чтобы утопить стержень, оставляя его в вертикальном положении?

Задача №3.3.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$l=1$ м, $S=1$ см², $h_0 = 0,8l$, $A-?$

Решение задачи:

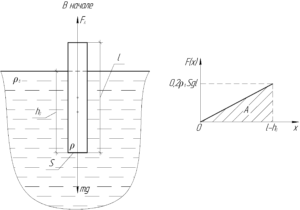Стержень плавает, запишет условие плавания тел:

$$mg = {F_А}$$

Распишем массу через плотность и полный объем, а силу Архимеда — по известной формуле:

$$\rho Slg = {\rho _в}gS{h_0}\;\;\;\;(1)$$

$$\rho l = {\rho _в}{h_0}$$

Так как $h_0 = 0,8l$, то:

$$\rho l = 0,8{\rho _в}l \Rightarrow \rho  = 0,8{\rho _в}$$

Чтобы утопить стержень, к нему нужно приложить внешнюю силу $F$. Для того, чтобы работа этой силы оказалось минимальной, стержень необходимо погружать с минимальной скоростью и ускорением. Понятно, что это величина этой силы будет переменной и зависеть от перемещения $x$, поскольку с увеличением погружения стержня на него будет действовать большая сила Архимеда. Из первого закона следует:

$$F\left( x \right) = {F_А}\left( x \right) — mg$$

$$F\left( x \right) = {\rho _в}gS\left( {{h_0} + x} \right) — \rho Slg$$

Видно, что внешняя сила зависит линейно от перемещения.

При $x=0$ внешняя сила $F$ тоже равна нулю (смотрите выражение (1)):

$$F\left( 0 \right) = {\rho _в}gS{h_0} — \rho Slg = 0$$

Когда стержень будет полностью погружен в воду, то есть при $x = \left( {l — {h_0}} \right)$, величина внешней силы $F$ определяется выражением:

$$F\left( {l — {h_0}} \right) = {\rho _в}gSl — \rho Slg = \left( {{\rho _в} — \rho } \right)Sgl$$

Так как мы уже знаем, что $\rho  = 0,8{\rho _в}$, то:

$$F\left( {l — {h_0}} \right) = 0,2{\rho _в}Sgl$$

Теперь, если построить график изменения внешней силы от перемещения, то площадь фигуры под графиком равна искомой работе $A$. Работа $A$ численно равна площади треугольника, поэтому:

$$A = \frac{1}{2} \cdot 0,2{\rho _в}Sgl \cdot \left( {l — {h_0}} \right)$$

По условию $h_0 = 0,8l$, поэтому:

$$A = 0,02{\rho _в}Sg{l^2}$$

Переведем площадь сечения в систему СИ и посчитаем ответ:

$$1\;см^2 = {10^{ — 4}}\;м^2$$

$$A = 0,02 \cdot 1000 \cdot {10^{ — 4}} \cdot 10 \cdot {1^2} = 0,02\;Дж = 20\;мДж$$

Ответ: 20 мДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.48 Однородный пробковый брусок квадратного сечения со стороной 10 см и длиной 40 см
3.3.50 Шарик для игры в настольный теннис радиусом 15 мм и массой 5 г погружен в воду
3.3.51 Два деревянных шара одинакового объема, полностью находящиеся в жидкости